算法分析

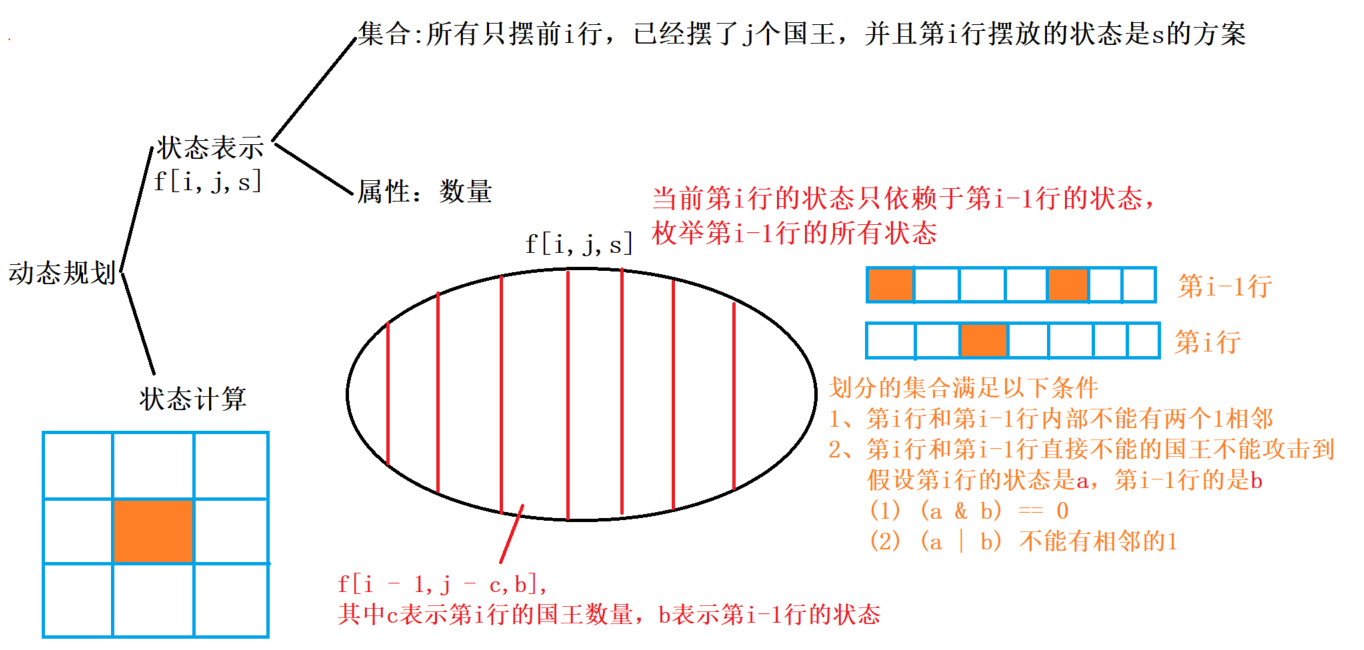
状态压缩dp

时间复杂度

上限复杂度是$O(n * m^2 * s * k)$，n表示行数，m^2表示国王填的数量，s表示合法状态数量，k表示合法状态的转移数量

参考文献

算法提高课

Java 代码

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {
    static int N = 12,M = 1 << N,K = 110;
    static int n,m;
    static List<Integer> state = new ArrayList<Integer>();
    static int[] cnt = new int[M];
    static ArrayList<Integer>[] head = new ArrayList[M];
    static long[][][] f = new long[N][K][M];
    //判断状态是否合法，没有相邻的1返回true，否则返回false
    static boolean check(int s)
    {
        for(int i = 0;i < n;i ++)
        {
            if((s >> i & 1) == 1 && (s >> i + 1 & 1) == 1)
                return false;
        }
        return true;
    }
    static int count(int s)
    {
        int res = 0;
        for(int i = 0;i < n;i ++) 
            if((s >> i & 1) == 1)
                res ++;
        return res;
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();

        for(int i = 0;i < 1 << n;i ++)
        {
            if(check(i))
            {
                state.add(i);
                cnt[i] = count(i);
            }
        }

        for(int i = 0;i < state.size();i ++)
        {
            head[i] = new ArrayList<Integer>();
            for(int j = 0;j < state.size();j ++)
            {
                int a = state.get(i);
                int b = state.get(j);
                if((a & b) == 0 && (check(a | b)))
                {
                    head[i].add(j);
                }
            }
        }

        f[0][0][0] = 1;
        for(int i = 1;i <= n;i ++)
            for(int j = 0;j <= m;j ++)
                for(int a = 0;a < state.size();a ++)
                    for(int b : head[a])
                    {
                        int c = cnt[state.get(a)];
                        if(j >= c) f[i][j][a] += f[i - 1][j - c][b];
                    }

        long res = 0;
        for(int i = 0;i < 1 << n;i ++) res += f[n][m][i];
        System.out.println(res);
    }
}