思路分析

该问题的难度在于，需要一步步想出多个子问题，且每个子问题的难度也不低，所以遇到一个问题时可能无法做到立马求解，需要想着如何把它拆解成子问题，再层层递进求解。

组合问题求最值：考虑用背包来做，该问题数据下，背包解法可能会超时，背包问题的复杂度是n*m = 340亿，会超时。

（1）考虑用暴搜解决，n（最大有34）个数：直接暴搜，每个数有选或不选两种选择，需要的时间为 2^34，题目给定时间为1s（能计算10亿次），，整棵dfs搜索树会非常大，会超时，考虑用双向dfs。分别对前n/2和后n/2个数数进行dfs，各自的时间为 2^17 ，此时得到两个集合A 和 B。
注意：由于两个集合中的元素的值可能会超过m，因此可以mod一个m，使得集合中元素的值在[0, m-1]之间。

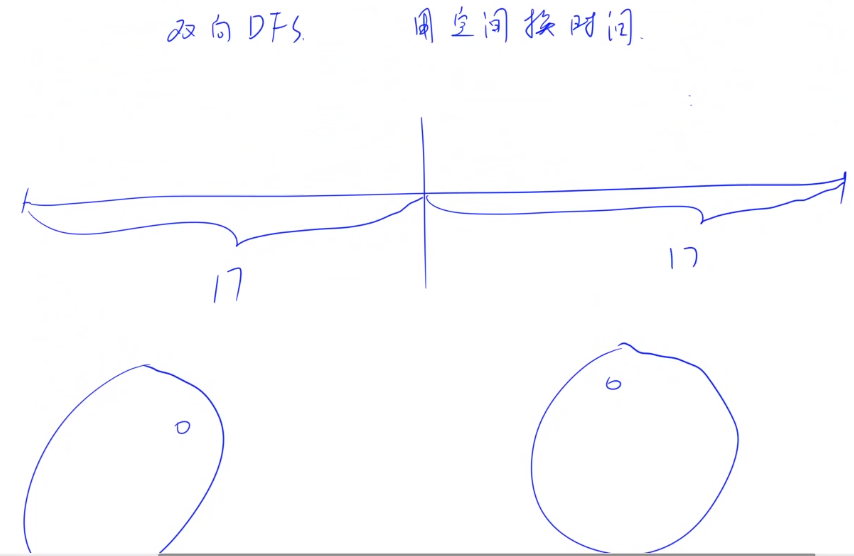
（2）然后在两个集合中每次各选一个元素拼起来求解，一共枚举n^2次，所得余数最大值即为所求。注意n^2次方会超时（2^17*2^17 = 2^34），因此需要一些技巧来降低复杂度。

（3）双指针技巧：
集合A和B中元素的取值范围都在[0, m-1]，因此A[i] + B[j] 的取值范围是[0,2m-2]，考虑到是求该序列中模上m后所得余数最大的元素，求解方法位先将该范围划分为：[0,…,m-1], [m, …, 2m-2]，再取两个区间内的余数最大值。此时复杂度为 2^17 * log2^17（排序）= 17 * 2^17.

• [m, …, 2m-2]：当A[i] + B[j]落在该区间内时，值越大，则所得的余数也就越大，分别取两个集合中的最大值即能得到。
• [0, …, m-1]：设立一个双指针，i从前往后遍历集合A，j从后往前遍历集合B，只有当A[i] + B[j] < m 时，才计算
  余数。
  

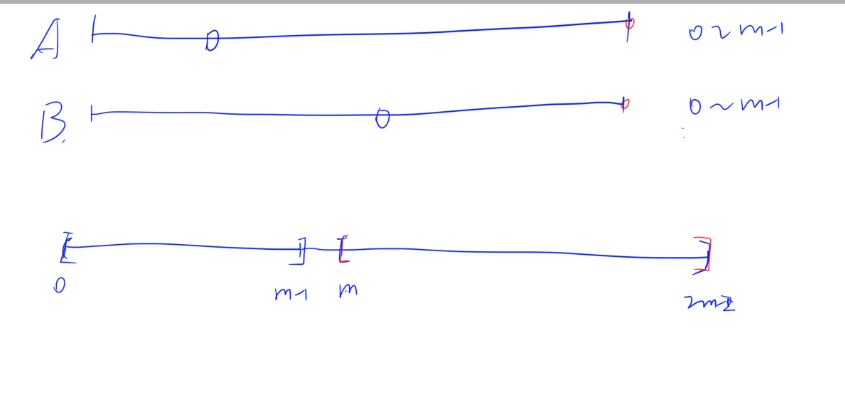
取两个区间内的最大余数，即为所求。
注意：用双针技巧前需要先对两个集合排序。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 34;
int n,m;
int w[N];

void dfs(int u, int k, int s, vector<int> &way)
{
    if(u == k) way.push_back(s);
    else
    {
        dfs(u+1, k, s, way); //不选第u个数
        dfs(u+1, k, (s+w[u]) % m, way); //选第u个数
    }
}

int main()
{
    cin>>n>>m;
    for(int i=0; i<n; i++) cin>>w[i];

    vector<int> A, B;
    dfs(0, n/2, 0, A); //dfs前n/2个数，把组合情况保存在集合A中
    dfs(n/2, n, 0, B);

    sort(A.begin(), A.end());
    sort(B.begin(), B.end());

    int res = (A.back(), B.back()) % m; //区间[m, ..., 2m-2]里的最大余数
    for(int i=0, j = B.size() -1; i<A.size(); i++)
    {
        while(j >=0 && A[i] + B[j] > m) j--;
        if(j >= 0) res = max(res, (A[i] + B[j]) % m);
    }

    cout<<res<<endl;
    return 0;
}