题目描述

Given a binary tree where each path going from the root to any leaf form a valid sequence, check if a given string is a valid sequence in such binary tree.

We get the given string from the concatenation of an array of integers arr and the concatenation of all values of the nodes along a path results in a sequence in the given binary tree.

样例

Example 1:

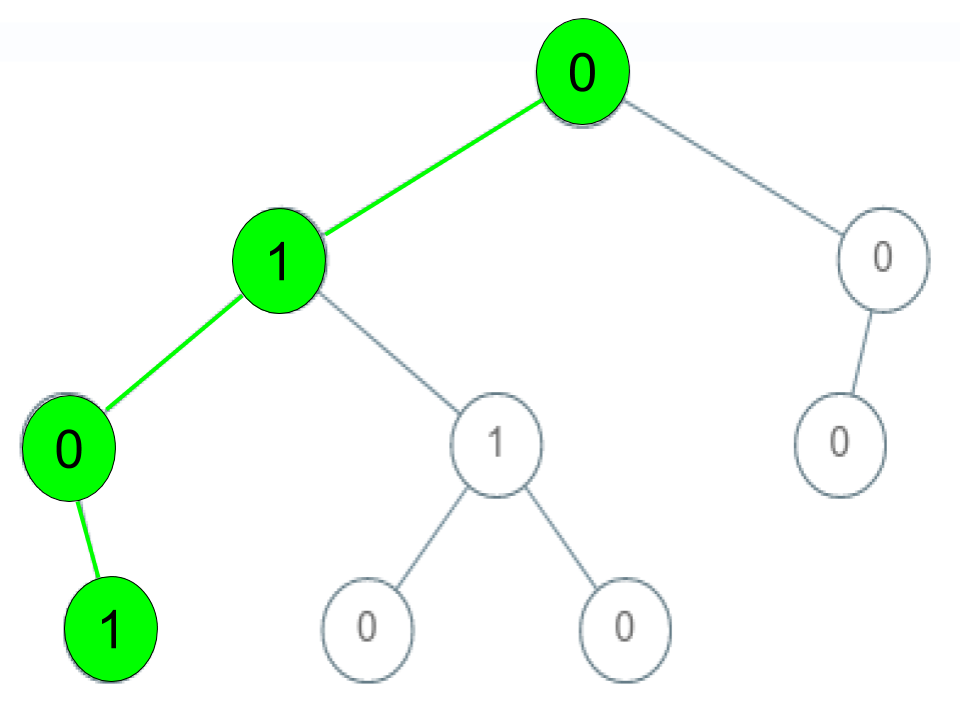
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,0,1]
Output: true
Explanation: 
The path 0 -> 1 -> 0 -> 1 is a valid sequence (green color in the figure). 
Other valid sequences are: 
0 -> 1 -> 1 -> 0 
0 -> 0 -> 0

Example 2:

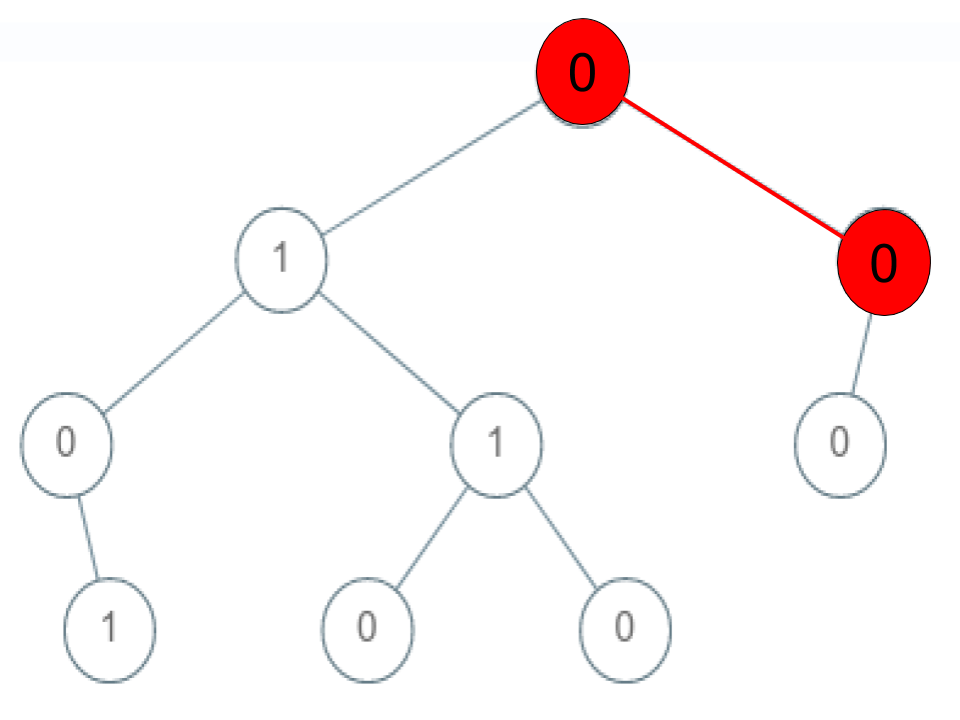
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,0,1]
Output: false 
Explanation: The path 0 -> 0 -> 1 does not exist, therefore it is not even a sequence.

Example 3:

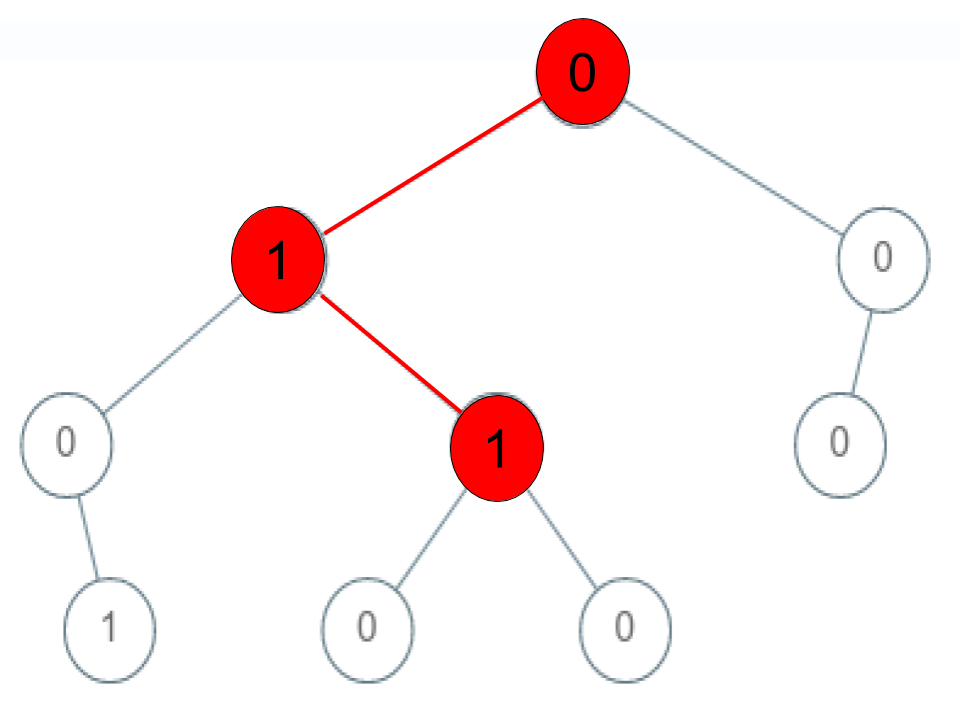
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,1]
Output: false
Explanation: The path 0 -> 1 -> 1 is a sequence, but it is not a valid sequence.

Constraints:

• 1 <= arr.length <= 5000
• 0 <= arr[i] <= 9
• Each node’s value is between [0 - 9].

算法

LeetCode打卡的一道题，没找到对应的题号，后面LeetCode出现题号后再修改

数据范围表明序列不为空，并且始终保证start <= end，一种很直接的思路就是检验当前点是否等于数组里对应的元素，于是我们用start来记录检验到数组的哪个位置，end是数组的边界。然后递归的检验树的左右节点。

既然涉及到递归，首先应该考虑递归的终止条件，终止的情况可能有：

• 树遍历到了叶节点（描述叶节点就是检验左右子树是否为空），数组也遍历到了最后一个元素，那么只需检验叶节点的值和数组元素值是否相等
• 树还没有到叶节点，但是数组已经到了末尾，为false
• 树到了叶节点，但是数组还没有到末尾，为false

考虑递归中可能存在的问题，因为终止情况已经检验了树节点为空的情况，那么此时树的节点不为空，只需要检验元素是否对应相等即可。最后递归遍历左右子树，结果取或即可。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidSequence(TreeNode* root, vector<int>& arr) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        int n = arr.size();
        return isValid(root, 0, n - 1, arr);
    }

    bool isValid(TreeNode *root, int start, int end, vector<int> & arr)
    {
        if (start == end && root && !root -> left && !root -> right)
            return root -> val == arr[start];
        if ((!root && start <= end) || (root && start > end)) return false;
        if (root -> val != arr[start]) return false;

        bool left = start < end ? isValid(root -> left, start + 1, end, arr) : false;
        bool right = start < end ? isValid(root -> right, start + 1, end, arr) : false;
        return left || right;
    }
};