思路：（这个题一定要捋清思路！）

树的重心是：将这个点删除后，剩余各个连通块中点数的最大值最小

所以：

1. 先求每个点的 所有连通块的点数的最大值 (cur_ans)
2. 再求 到底是哪个点的(最大)值最小 (ans)

步骤：

1. 先求每个点的 所有连通块的点数的最大值 (cur_ans)

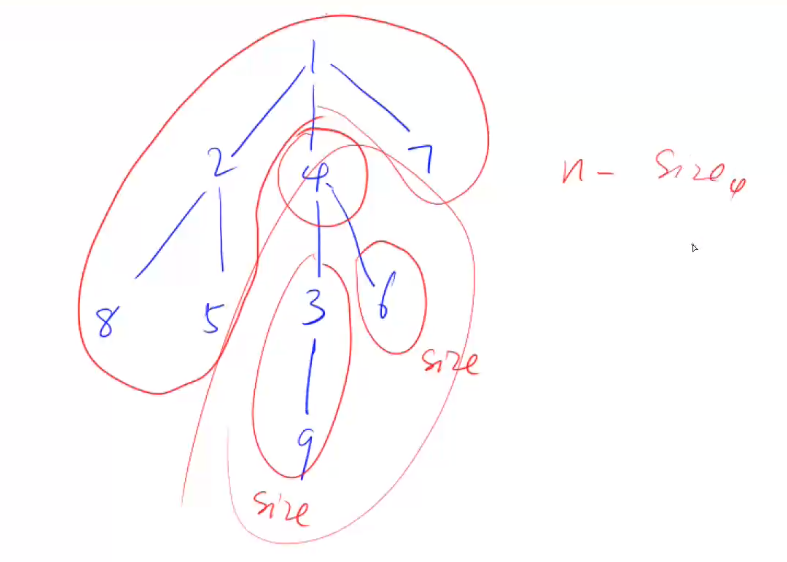
问题1. 如何求一个点的各个连通块的点数

dfs(int u) 求的是：以u为根的各个子树(删掉了根就是连通块)的点的数量
每求一棵子树就:

int s = dfs(u);
cur_ans = max(cur_ans, s);
sum += s;  // (可以看完问题2再看)

问题2. 除了这棵树对应的连通块，剩下的点怎么求

剩下的点自动成为一个连通块，所以用 n - 树的节点个数 即为剩下的节点个数
那么树的结点个数怎么求呢？

答： 可以在dfs里定义一个 int sum = 1，表示以u为根的树的节点个数，树的初始状态是有一个根节点，所以初始为1。
每求出一个连通块的点数就sum += s(这回在看一下问题1)

然后cur_ans: 得出对于u点的所有连通块中(树+除了树) 点数的最大值。

cur_ans = max(cur_ans, n - sum);

2. 求 到底是哪个点的(最大)值最小 (ans)

ans = min(ans, cur_ans);

Note:

1. 这个题相当于无向图
   对于无向图，应该是有向图的边数*2，所以这里M = 2 * N
2. int ans = N 来更新答案
3. 用过的点标记为st[u] = true;
4. dfs返回的是 sum

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 100010, M = N * 2;  // 无向图，存双边

int n;
int h[N], ne[M], idx, e[M];  // 这个也是因为 a->b, b->a 都得存
int ans = N;  // ans就是各个点对应的cur_ans的最小值
bool st[N];


void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs(int u)
{
    st[u] = true;

    int sum = 1;  // u的这棵子树里的点的个数。记录这个是为了算除了以u为树的剩余节点组成的连通块的点的数量
    int cur_ans = 0;  // cur_ans 记录的是以u为根的子树的连通块中点数的最大值
    for (int i = h[u]; i != -1 ; i = ne[i] )
    {
        int j = e[i];
        if(!st[j])
        {
            int s = dfs(j);
            cur_ans = max(cur_ans, s);  // 每走一次算一次最大值

            sum += s;  
        }        
    }

    cur_ans = max(cur_ans, n - sum);

    ans = min(ans, cur_ans);

    return sum;
}

int main()
{
    cin >> n;

    memset(h, -1, sizeof h);

    for (int i = 0; i < n ; i ++ )
    {
        int a, b;
        cin >> a >> b;

        add(a, b), add(b, a);
    }

    dfs(1);

    cout << ans << endl;

    return 0;
}