题目描述

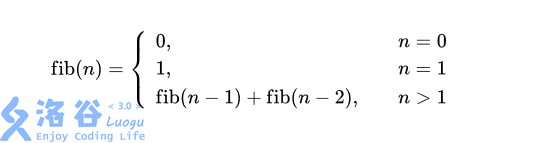
试求出$Fib_n$

样例

输入：

5

输出：

5

算法1

(暴力递推) $O(n)$

想要存储他，很多人会想到用一维数组存储+递推。递推初值为$Fib_0=0$,$Fib_1=1$。递推式为$Fib_n=Fib_{n-1}+Fib_{n-2}$代码也很好实现：

int n;
cin>>n;
f[0]=0,f[1]=1;
for(int i=2;i<=n;i++) f[i]=f[i-1]+f[i-2];
cout<<f[n];

算法2

(暴力递推+空间优化) $O(n)$

可以将上面代码优化一下，$Fib_n$只和$Fib_{n-1}$与$Fib_{n-2}$有关系，所以不用数组存，用字母$a,b,c$代替即可。代码如下：

int n;
cin>>n;
int a=0,b=1;
for(int i=2;i<=n;i++) {
    c=a+b;//a相当于f[n-2],b相当于f[n-1] 
    a=b;
    b=c;
}
cout<<c;

算法3

(求递推公式) $O(1)$

我慢慢要显露出数竞生本色啦！

其实不难发现，斐波那契就是$a_n=pa_{n-1}+qa_{n-2}$的特例，不过$a_n=pa_{n-1}+qa_{n-2}$有点难，我们需要一点点前置知识：

$step\ 1$ ：$a_n=pa_{n-1}$，这是个等比数列，直接过掉。

解：$a_n=pa_{n-1}=p^2a_{n-2}=…=p^{n-1}a_1$

$step\ 2$ ：$a_n=pa_{n-1}+q$，尝试转化为等比数列。

解：待定系数。令$a_n+t=p(a_{n-1}+t)$解出$t$即可。

$step\ 3$ ：$a_n=pa_{n-1}+qa_{n-2}$。

要讲明白特征方程是怎么回事实在是太麻烦了，笔者手写了三页，但最后字迹过于丑陋，不宜展示。

我认为这里写的不错，可以参考。

综上，通项公式为：

让我们重新审视题目。

经过前面的铺垫，相信你已经可以写出代码了：

自己写写看呗
注意小数问题呦

练习题：洛谷P4994。

一个个 OIer 的竞赛生涯总是从一场 NOIp 开始，大多也在一场 NOIp 中结束，好似一次次轮回在不断上演。

如果这次 NOIp 是你的起点，那么祝你的 OI 生涯如同夏花般绚烂。

如果这次 NOIp 是你的终点，那么祝你的 OI 回忆宛若繁星般璀璨。

也许这是你最后一次在洛谷上打比赛，也许不是。

不过，无论如何，祝你在一周后的比赛里，好运。