题目

分析

动态规划

这道题可以用动态规划的思路去求解

闫氏dp分析法

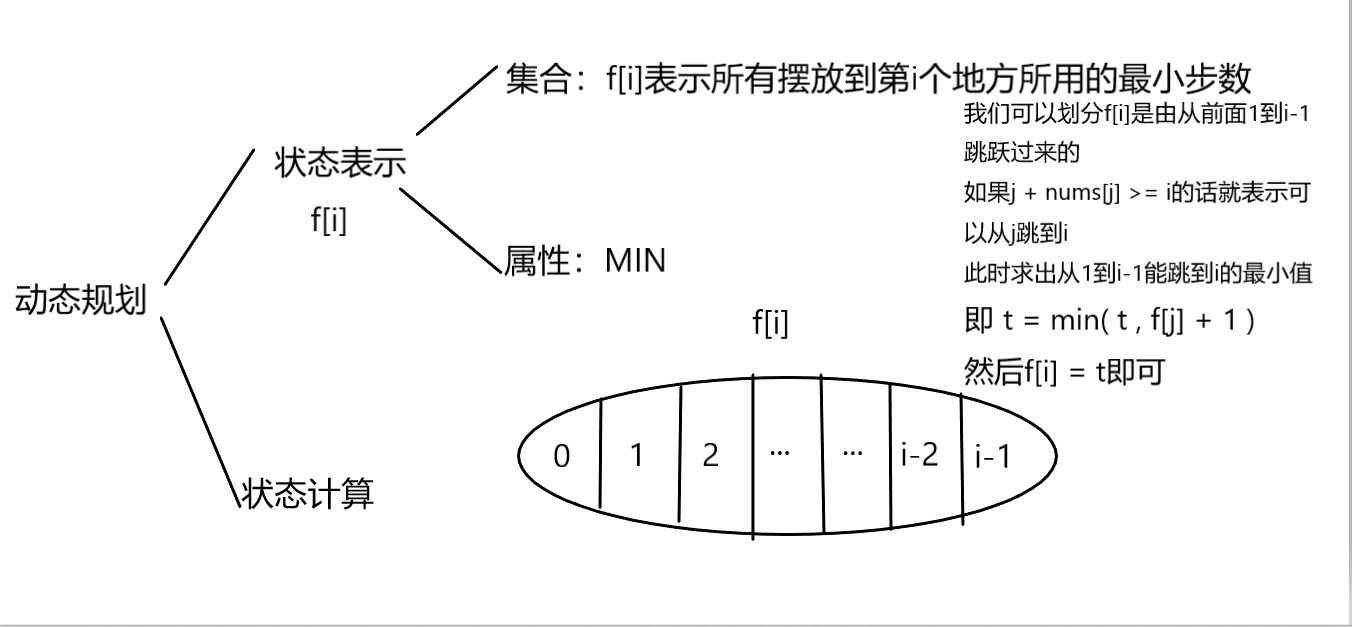
对应的dp代码就是

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int>f(n+1);
        for(int i = 1;i < n;i++)
        {
            int t = INT_MAX;
            for(int j = 0;j < i;j++)
            {
                if(j + nums[j] >= i)
                {
                    t = min(t,f[j]+1);
                }
            }
            f[i] = t;
        }

        return f[n-1];
    }
};

但是很显然，这样dp最坏的情况下时间复杂度会达到O(n^2)会超时

这个时候我们就需要思考应该怎么样改进我们的代码了

贪心 + 动态规划

通过枚举单纯的动态规划我们可以知道，f[N]数组里面是单调递增的
大概就是0,1,1,2,2,2,....
所以f[i]是一个单调递增的数组
又从动态规划的状态转移方程可知
f[i] = f[j] + 1
我们要枚举i之前的能跳到i的所有j，然后每次找到一个符合条件的j之后就f[i] = f[j]+1
因为初始的时候f[j]都为0，所以不管找到多少个j，都只会使得f[i]在0的基础上加1

找到第一个能跳到i的j的时候更新了一次f[i]，之后无论再找到多少个j都只能使得f[i] = 0+1 = 1
也就是说除了第一个点之外，后面找到的点都是进行的重复的操作

所以我们只用找到第一个能跳到i的点j，然后用j去更新i的状态即f[i] = f[j] + 1

后面更新更多的点同理，只用找到能跳到的第一个点即可

动态规划时瓶颈就在于更新每个点的最小值时需要遍历所有能跳到i的点，而有了单调性以后就可以用第一个能跳到i的点更新了

因为找到第一个点和遍历所有的点都只遍历了一次，所以时间复杂度会降到O(n)

对应的代码

class Solution {
public:
    int jump(vector<int>& nums) {
        int n = nums.size();
        vector<int>f(n+1);
        for(int i = 1,val = 0;i < n;i++)
        {
            while(val < i && val + nums[val] < i) val++;//找到能跳到i的第一个点
            f[i] = f[val] + 1;//直接更新f[i]
        }

        return f[n-1];
    }
};