这是我写的一篇分享:KMP 算法详解 搬过来的。
本文介绍字符串匹配之 KMP 算法。
写在前面
KMP 算法用于解决字符串的单模匹配问题,即在一个主串 $\rm S$ 中查找模式串 $\rm P$ 的所有出现位置,该算法解决此问题的时间复杂度为 $O(|\rm S|+|\rm P|)$。
本文不再介绍暴力做法以及字符串哈希解法。
KMP 算法
在 KMP 算法中,有一个很重要的数组,叫做 $\rm Next$ 数组(也有地方叫 $\rm Fail$ 数组或者前缀函数)。$\rm Next$ 数组巧妙地利用了模式串 $\rm P$ 中以某个位置结尾的后缀的与 $\rm P$ 的前缀匹配的信息,来加速 $\rm P$ 在 $\rm S$ 中的匹配过程。
Next 数组的性质
$\mathrm{Next}[i]$ 表示模式串 $\rm P$ 中以 $i$(下标从 $1$ 开始)结尾的真后缀1能匹配 $\rm P$ 的前缀的最大长度。
$$ \mathrm{Formally},\ \mathrm{Next}[i]=\max_{1 \le j \le i-1} \lbrace j\rbrace \ \mathrm{while}\ \mathrm{P}[1:j]==\mathrm{P}[i-j+1:i] $$
| $\rm P$ | a | b | a | b | a |
|---|---|---|---|---|---|
| $i$ | 1 | 2 | 3 | 4 | 5 |
| $\rm Next[i]$ | 0 | 0 | 1 | 2 | 3 |
请务必理解上表,并且要时刻记得 $\rm Next[\ ]$ 表示的是模式串 $\rm P$ 的信息。
我们先不考虑 $\rm Next[\ ]$ 如何求解,而是看看它有什么性质,接下来,我将从较宏观的角度2来解释,而不是通过具体的实例来分析。
现在我们有一个字符串 $\rm P$,并且已知了 $\rm Next[\ ]$ 数组。有 $\mathrm{Next}[i]=j$, $\mathrm{Next}[j]=k$。
那么有一个显然的性质:$k<j<i$,然后我们可以画出下面的示意图:
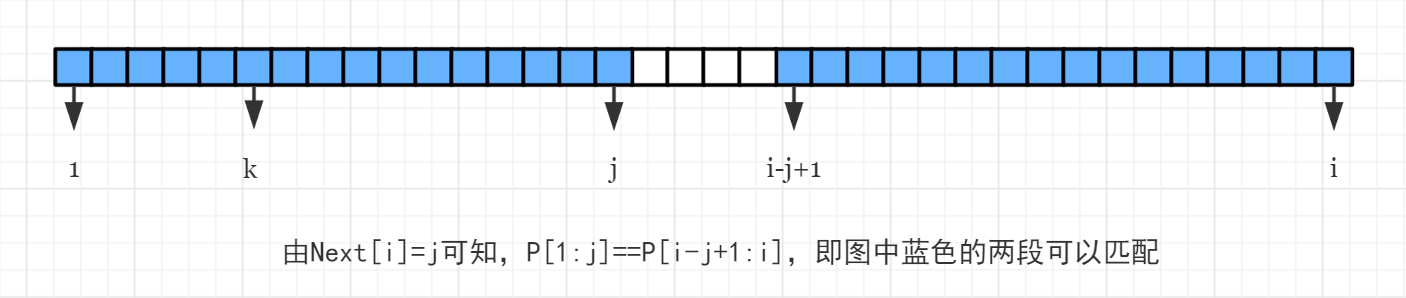
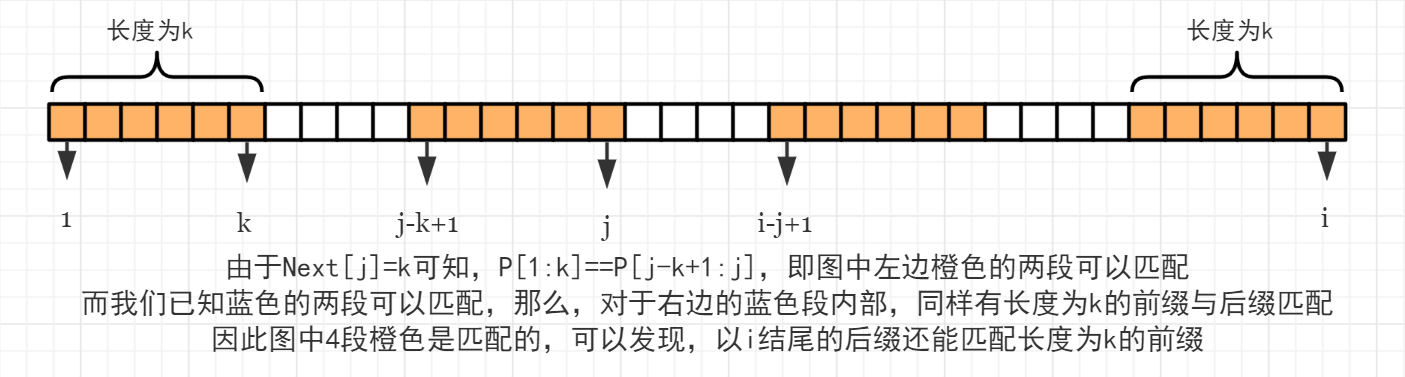
也就是说,若以 $i$ 结尾的真后缀能匹配 $\rm P$ 的前缀的最大长度为 $\mathrm{Next}[i]$,那么它能匹配的次长前缀长度为 $\mathrm{Next[Next}[i]]$,以此类推,$\mathrm{Next[Next[Next}[i]]] \cdots$ 直至匹配长度为 $0$ 为止。
这是一条很重要的性质,是KMP算法的关键,它与模式串 $\rm P$ 在主串 $\rm S$ 中发生失配时的下一步操作有关。
KMP 匹配过程
下面我们举个例子来演示 $\mathrm{Next}[\ ]$ 在匹配过程中的作用。
已知主串 $\rm S$ 和模式串 $\rm P$,且 $\rm P$ 的 $\mathrm{Next}[\ ]$ 数组已经求出来了,当前主串 $\rm S$ 匹配到下标 $i-1$ 位置,模式串 $\rm P$ 匹配到下标 $j$ 位置,即满足 $\mathrm{S}[i-j:i-1]==\mathrm{P}[1:j]$,如下图所示:
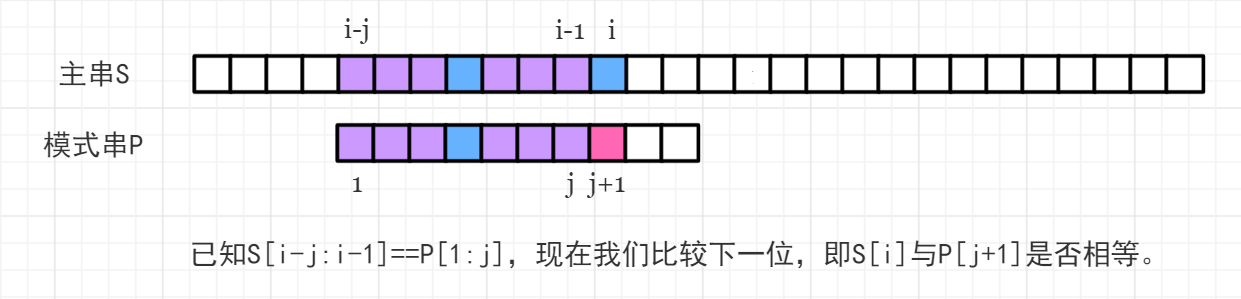
- $\mathrm{S}[i] == \mathrm{P}[j+1]$,则 $j$ 后移一位,表示这一位匹配成功,此时如果 $j$ 到达了 $\rm P$ 串的末尾,说明 $\rm P$ 在 $\rm S$ 中出现了,在 $\rm S$ 中的起始下标为 $i-|\mathrm{P}|+1$。
- $\mathrm{S}[i] \neq \mathrm{P}[j+1]$,发生失配,此时难道我们需要从头开始匹配吗?不需要,我们已经知道了 $\rm P$ 中以 $j$ 结尾的后缀已经能与 $\rm S$ 中以 $i-1$ 结尾的后缀能够匹配,我们希望 $\rm P$ 串向右移动最少,即希望..移动后.. $\rm P$ 的前缀能与 $\rm S$ 中以 $i-1$ 结尾的后缀匹配尽可能长,而 $\rm S$ 中以 $i-1$ 结尾的后缀又等效于 $\rm P$ 中以 $j$ 结尾的后缀,这恰好就是 $\mathrm{Next}[j]$ 的含义,$\mathrm{S}[i-\mathrm{Next}[j]:i-1]==\mathrm{P}[1:\mathrm{Next}[j]]$,也就是图中标记的紫色部分匹配。那么只要将 $\rm P$ 中第一段紫色移动到第二段位置即可,如下图所示:
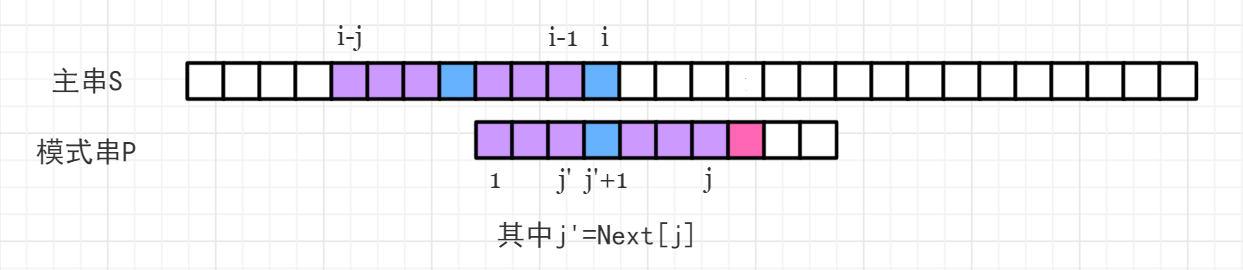
上述移动的过程,就是令 $j=\mathrm{Next}[j]$。然后我们只需要再比较 $\mathrm{S}[i]$ 与 $\mathrm{P}[j+1]$ 是否匹配即可。如果不匹配就需要不断回退 $j=\mathrm{Next}[j]$,其实就是不断用 $\mathrm{P}$ 中已经能与 $\rm S$ 中以 $i-1$ 结尾的后缀匹配的前缀,减少中间多余匹配过程,在不断失配的过程中,所使用的 $\rm P$ 的前缀长度递减,直至为 $0$。如果经过某次 $j$ 的回退,满足了 $\mathrm{S}[i]==\mathrm{P}[j+1]$,那么 $j$ 就可以后移了。图中表现的是,经过一次回退,就能成功匹配的情况(都是蓝色的小方块)。
以上就是 KMP 算法的匹配过程,代码如下:
/* n为模式串p的长度,m为主串s串的长度 */
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = Next[j]; /* 失配j就不断回退 */
if (s[i] == p[j + 1]) j++; /* 匹配成功j后移 */
if (j == n) { /* p在s中完整出现 */
cout << i - n + 1 << " "; /* 出现的起始位置 */
j = Next[j]; /* 防止下一轮匹配时j+1越界 */
}
}
Next 数组求解
理解了上述匹配过程,$\rm Next[\ ]$ 的求解就不难理解了。我们可以把 $\rm Next[\ ]$ 的求解过程看成是两个相同的串 $\rm P$ 匹配的过程,也可以看成模式串 $\rm P$ 自身与自身匹配的过程。
首先对于 $\rm P$ 串,显然有 $\mathrm{Next}[1]=0$(因为只考虑..真..前/后缀),然后两个指针 $i=2,j=0$ 开始,考虑 $\mathrm{P}[i]$ 与 $\mathrm{P}[j+1]$ 是否匹配,如果不匹配,那么 $j=\mathrm{Next}[j]$ 不断回退,直到回退到匹配长度为 $0$ 或者某一个 $j$ 能满足 $\mathrm{P}[i]==\mathrm{P}[j+1]$;如果 $\mathrm{P}[i]==\mathrm{P}[j+1]$,$j$ 后移,说明以 $\rm P$ 中以 $i$ 结尾的真后缀能匹配 $\rm P$ 的前缀的最大长度为 $j$,因此 $\mathrm{Next}[i]=j$。是不是与 KMP 匹配过程如出一辙呢?代码如下:
Next[1] = 0; /* 全局变量时可省略 */
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = Next[j];
if (p[i] == p[j + 1]) j++;
Next[i] = j; /* 更新Next */
}
完整代码
题目链接:AcWing 831. KMP字符串
#include <iostream>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
char p[N], s[M];
int Next[N];
int main() {
cin >> n >> p + 1 >> m >> s + 1;
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = Next[j];
if (p[i] == p[j + 1]) j++;
Next[i] = j;
}
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = Next[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
printf("%d ", i - n); /* 本题下标从0开始,与上文不同 */
j = Next[j];
}
}
return 0;
}
时间复杂度分析
$\mathrm{Next}[\ ]$ 求解与 KMP 匹配的时间复杂度分析类似,这里就分析一下 KMP 的匹配过程的时间复杂度。首先,在每次i++的过程中,j最多只会增加一次,因此j总共最多增加 $|\rm S|$ 次,而while循环中j总共的回退次数不可能超过它增加的次数,因此while循环中j最多回退 $|\rm S|$ 次,所以 KMP 匹配过程时间复杂度为 $O(|\rm S|)$。$\mathrm{Next}[\ ]$ 求解时间复杂度为 $O(|\rm P|)$。
因此,整个算法的总时间复杂度为 $O(|\rm S| + |\rm P|)$。
特别鸣谢
- AcWing 算法基础课
- 时间复杂度分析:皎月半洒花的题解


666~这一篇讲得很清晰
谢谢大佬orz orz