算法1

(二分) $O(logn)$

利用二分，找到上下界。
思路大家都知道，但是怎么写出来就是个问题了。
目标值是3：arr[mid] > 3 的话R = mid - 1; ，arr[mid] < 3 的话L = mid + 1;

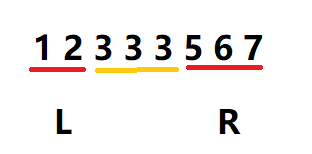
如果arr[mid] == 3 ,根据我们的需求来决定
如果想要找到下界，也就是最右边的3，那么左边的3就不关心 。
R = mid;后，最右边的3 还在[L,R]中

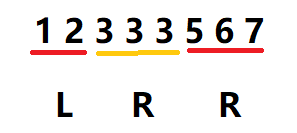
大于和等于的情况都需要改变R，小于的情况要改变L

while(L < R){
    int mid = L + R >> 1;
    if(arr[mid] >= k) R = mid;
    else L = mid + 1;
}

如果想要找到下界，也就是最左边的3，那么右边的3我们就不关心。
L = mid; 后，最左边的3 还在[L,R]中

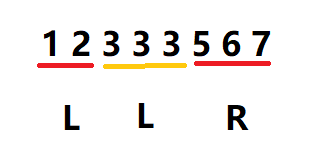
小于和等于的情况都要改变L,大于的情况要改变R (为了避免死循环，出现减法了要在计算mid的时候+1)

while(L < R){
    int mid = L + R + 1 >> 1;
    if(arr[mid] <= k) L = mid;
    else R = mid - 1;
}

java 代码

import java.util.*;
public class Main{
    static int arr[] = new int[100010], q = 0, k = 0, n = 0;
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        q = sc.nextInt();
        for(int i = 0; i < n; i++){
            arr[i] = sc.nextInt();
        }
        while(q-- != 0){
            k = sc.nextInt();
            int l = 0, r = n - 1, a = 0, b = 0;
            while(l < r){
                int mid = l + r >> 1;
                if(arr[mid] >= k) r = mid;
                else l = mid + 1;
            }
            a = i;
            l = 0;
            r = n - 1;
            if(arr[l] != k){
                System.out.println("-1 -1");
                continue;
            }
            while(l < r){
                int mid = l + r + 1>> 1;
                if(arr[mid] <= k) l = mid;
                else r = mid - 1;
            }
            b = l;
            System.out.println(a + " " + b );
        }
    }

}