题目描述

总共有 n 个人和 40 种不同的帽子，帽子编号从 1 到 40 。

给你一个整数列表的列表 hats ，其中 hats[i] 是第 i 个人所有喜欢帽子的列表。

请你给每个人安排一顶他喜欢的帽子，确保每个人戴的帽子跟别人都不一样，并返回方案数。

由于答案可能很大，请返回它对 10^9 + 7 取余后的结果。

样例

输入：hats = [[3,4],[4,5],[5]]
输出：1
解释：给定条件下只有一种方法选择帽子。
第一个人选择帽子 3，第二个人选择帽子 4，最后一个人选择帽子 5。

输入：hats = [[3,5,1],[3,5]]
输出：4
解释：总共有 4 种安排帽子的方法：
(3,5)，(5,3)，(1,3) 和 (1,5)

输入：hats = [[1,2,3,4],[1,2,3,4],[1,2,3,4],[1,2,3,4]]
输出：24
解释：每个人都可以从编号为 1 到 4 的帽子中选。
(1,2,3,4) 4 个帽子的排列方案数为 24 。

输入：hats = [[1,2,3],[2,3,5,6],[1,3,7,9],[1,8,9],[2,5,7]]
输出：111

提示：

• n == hats.length
• 1 <= n <= 10
• 1 <= hats[i].length <= 40
• 1 <= hats[i][j] <= 40
• hats[i] 包含一个数字互不相同的整数列表。

算法分析

状态压缩dp
由于人的个数是10，帽子个数是40，因此需要对人进行压缩，让人去匹配帽子

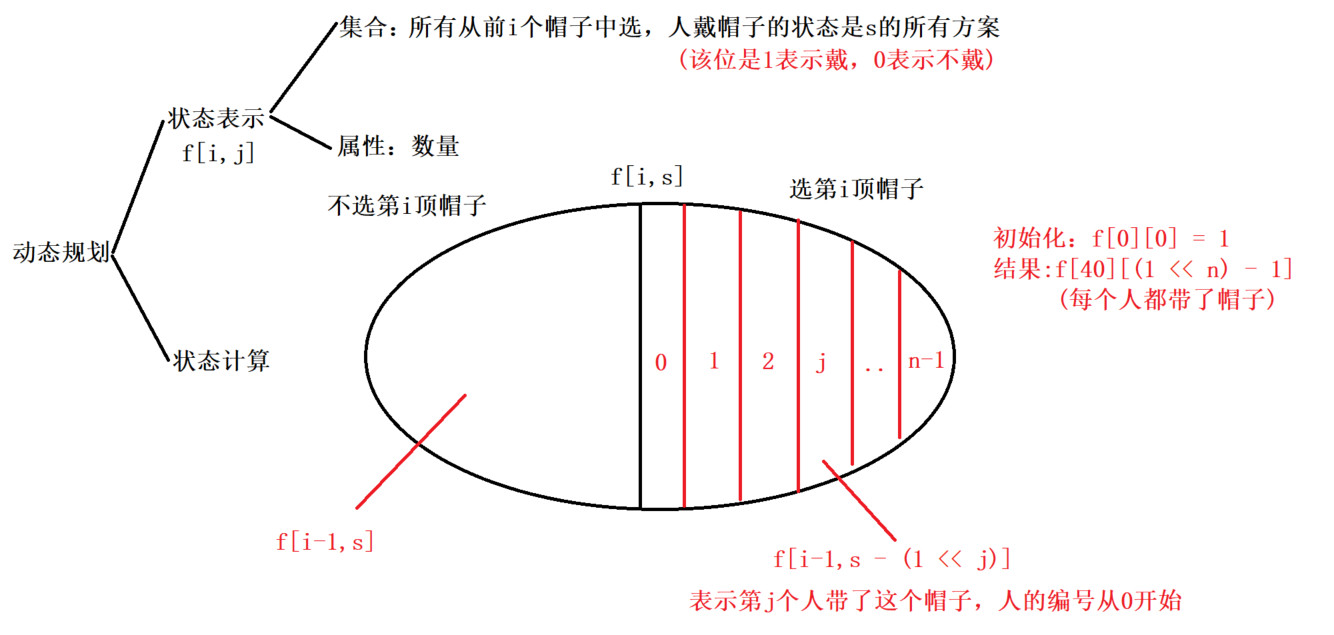
时间复杂度$O(40n2^n)$

Java 代码

class Solution {
    static int mod = 1000000000 + 7;
    public int numberWays(List<List<Integer>> hats) {
        boolean[][] like = new boolean[15][45];//表示第i个人喜欢第j顶帽子
        int[][] f = new int[45][1 << 11];
        int n = hats.size();
        for(int i = 0;i < n;i ++)
        {
            for(int k : hats.get(i))
            {
                like[i][k] = true;
            }
        }
        f[0][0] = 1;
        for(int i = 1;i <= 40;i ++)
        {
            for(int s = 0;s < 1 << n;s ++)
            {
                f[i][s] = f[i - 1][s];
                for(int j = 0;j < n;j ++)
                {
                    if(((s & (1 << j)) != 0) && like[j][i])
                        f[i][s] = (f[i][s] + f[i - 1][s - (1 << j)]) % mod;
                }

            }
        }
        return f[40][(1 << n) - 1];
    }
}