鄙人不才,此中鄙陋甚多,望海涵!
题中要求以中序遍历为1 2 3 4 5 ... n的顺序构造二叉树,这也是为何此题是一道区间dp题的原因,(若是没有这个要求的话样例5 7 1 2 10的答案绝对不是145),基本思路是在许多子区间找到根节点并记录更新(此处我就不再赘述,前佬之述备矣!)
这里我主要是想介绍这三种遍历的方式各自特征。
首先来解释一下题目中这个以12345...n中序遍历的意思!
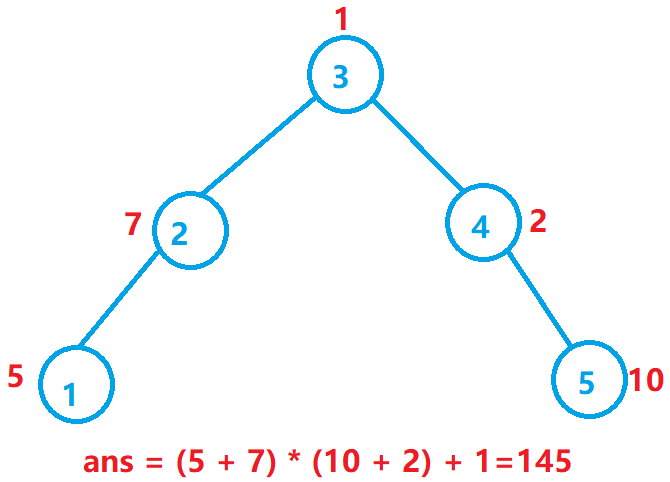
这算是符合题中要求的一种,从中我们不难发现节点下标小的都在大的左边(按12345...n来中序遍历),我们再来列举几个符合题意的中序遍历以便更好的理解。
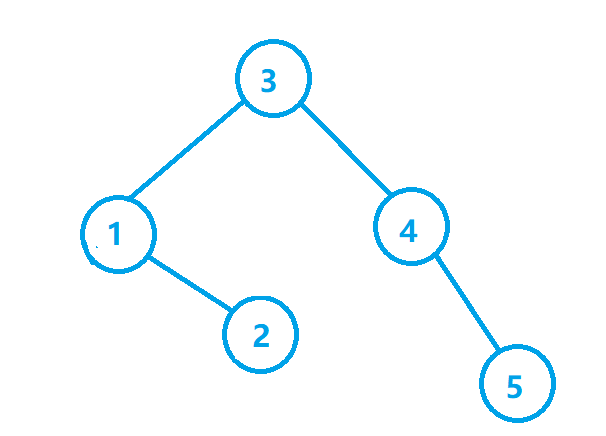
这个也是符合中序遍历要求的一种。
我们不妨以第一个图为例,对它进行三次遍历.
前序:(根节点优先,同级先左后右)3 2 1 4 5
中序:(先左后根最后右)1 2 3 4 5(这也是最重要的一种方式)
在这里我们为了更清楚的介绍中序遍历,引用一下CSDN作者翟光小朋友的图解
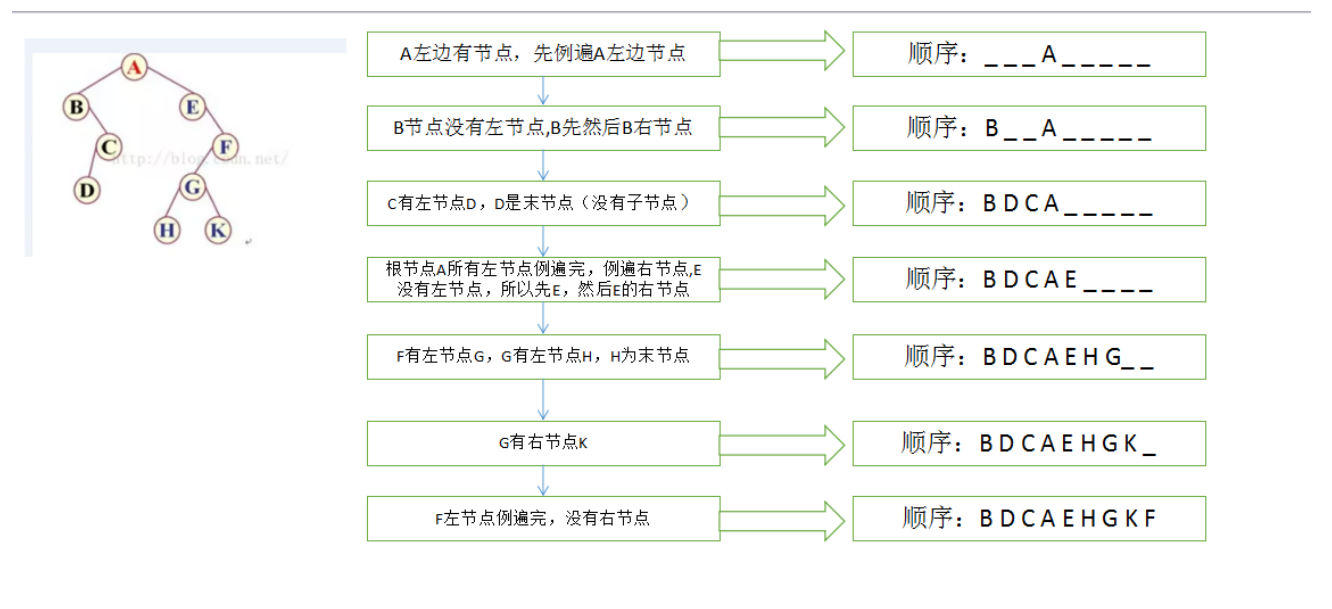


所以说五个点用中序遍历可以生成很多种情况吗,有些合理有些不合理(就是数字不够大
)
想问一下中序遍历能确定的树的数量是不是n!棵
这个我不太确实,但我试了试3个点的,只有5种,好像也不是n的阶乘,是5种吧,不过4个点的好像是24
真棒
哈哈哈,谢谢。