关于树的非递归遍历

结论：

用栈模拟实现中序遍历，Push操作的数据过程是先序遍历，Pop操作的数据过程是中序遍历

解析：

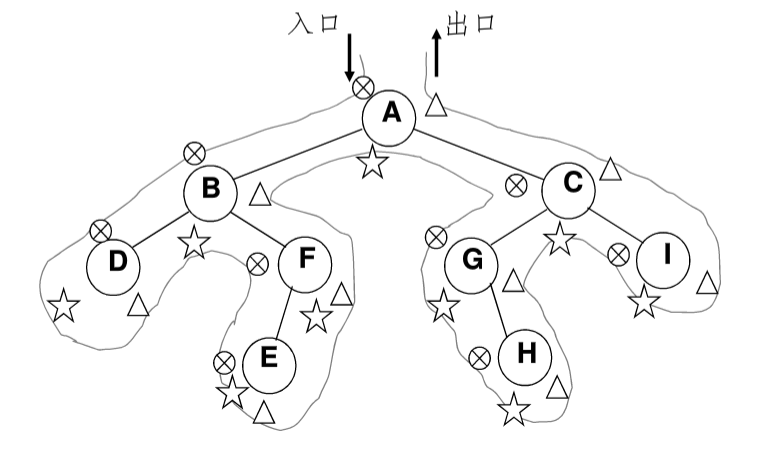
如图，常见的树的遍历方式（包括前序、中序、后序），实际上是将整棵树以这样的路线跑了1遍，只是碰到的时机不同。
综合来看每个结点都碰到了3次，分别标注了不同的符号，其中⊗是先序遍历，☆是中序遍历，△是后序遍历。
现在我们考虑非递归方式实现中序遍历：使用堆栈。

算法：

遇到一个结点，就把它压栈，并去遍历它的左子树。
当左子树遍历结束后，从栈顶弹出这个结点。
然后按其右指针再去中序遍历该结点的右子树。

代码：

void InorderTraversal (BinTree BT){
    BinTree T = BT;
    stack<int> st;
    while(T||!st.empty()){//树不空且堆栈不空
        while(T){
            st.push(T);//此处相当于图中第一次碰到结点
            T=T->left;//一直往左走
        }
        if(!st.empty()){
            printf("%d",st.top());//访问操作
            st.pop();//此处相当于图中第二次碰到结点
            T=T->right;//转向右子树
        }
    }
}

如果要用非递归的方式实现前序遍历呢？

只需要把访问操作的代码提前，改到第一次碰到结点的位置即可。

如果要用非递归的方式实现后序遍历呢？

在不修改结点结构的情况下，可以采取二次入栈，相当于图中第三次碰到结点时进行访问操作。

那么非递归层序遍历怎么办？

建议使用队列模拟。

本题参考解法： 前序遍历+中序遍历假建树的方式进行后序遍历

#include<iostream>
#include<cstring>
#include<algorithm>
#include<stack>
#include<vector>
#include<sstream>

using namespace std;
int n;
vector<int> preorder,inorder,postorder;
stack<int> st;

void build(int inL, int inR, int preL,int preR){//假建树
    if(inL>inR) return ;
    int root=preorder[preL];
    int k;
    for(k=inL;k<=inR;k++){
        if(inorder[k]==root){
            int numLeft=k-inL;
            build(inL,k-1,preL+1,preL+numLeft);
            build(k+1,inR,preL+numLeft+1,preR);
            postorder.push_back(root);
        }
    }
}

int main(){
    scanf("%d\n",&n);
    for(int i=0;i<n*2;i++){
        string str;
        getline(cin,str);
        stringstream ssin(str);//字符串流
        string a,b;
        ssin>>a>>b;
        if(a=="Push"){//说明是Push,Push顺序就是前序遍历
            preorder.push_back(stoi(b));
            st.push(stoi(b));
        }else{//pop出来模拟的是中序遍历
            inorder.push_back(st.top());
            st.pop();
        }
    }

    build(0,n-1,0,n-1);
    for(int i=0;i<n;i++){
        if(i==0)    printf("%d",postorder[i]);
        else    printf(" %d",postorder[i]);
    }

    return 0;
}

看起来更简洁的版本

#include<iostream>
#include<cstring>
#include<vector>
#include<stack>

using namespace std;
const int N=40;
int n;
vector<int> pre,in,post;
stack<int> st;

void build(int inL,int inR,int preL,int preR){
    if(inL>inR) return ;
    int root=pre[preL];
    int k;
    for(k=inL;k<=inR;k++)
        if(in[k]==root)
            break;
    if(k>inL)   build(inL,k-1,preL+1,preL+k-inL);
    if(k<inR)   build(k+1,inR,preL+k-inL+1,preR);
    post.push_back(root);
}

int main(){
    cin>>n;
    for(int i=0;i<n*2;i++){
        string str;
        cin>>str;
        int x;
        if(str=="Push"){
            cin>>x;
            pre.push_back(x);
            st.push(x);
        }else{
            x=st.top();
            in.push_back(x);
            st.pop();
        }
    }
    build(0,n-1,0,n-1);
    cout<<post[0];
    for(int i=1;i<n;i++)
        cout<<" "<<post[i];
    return 0;
}