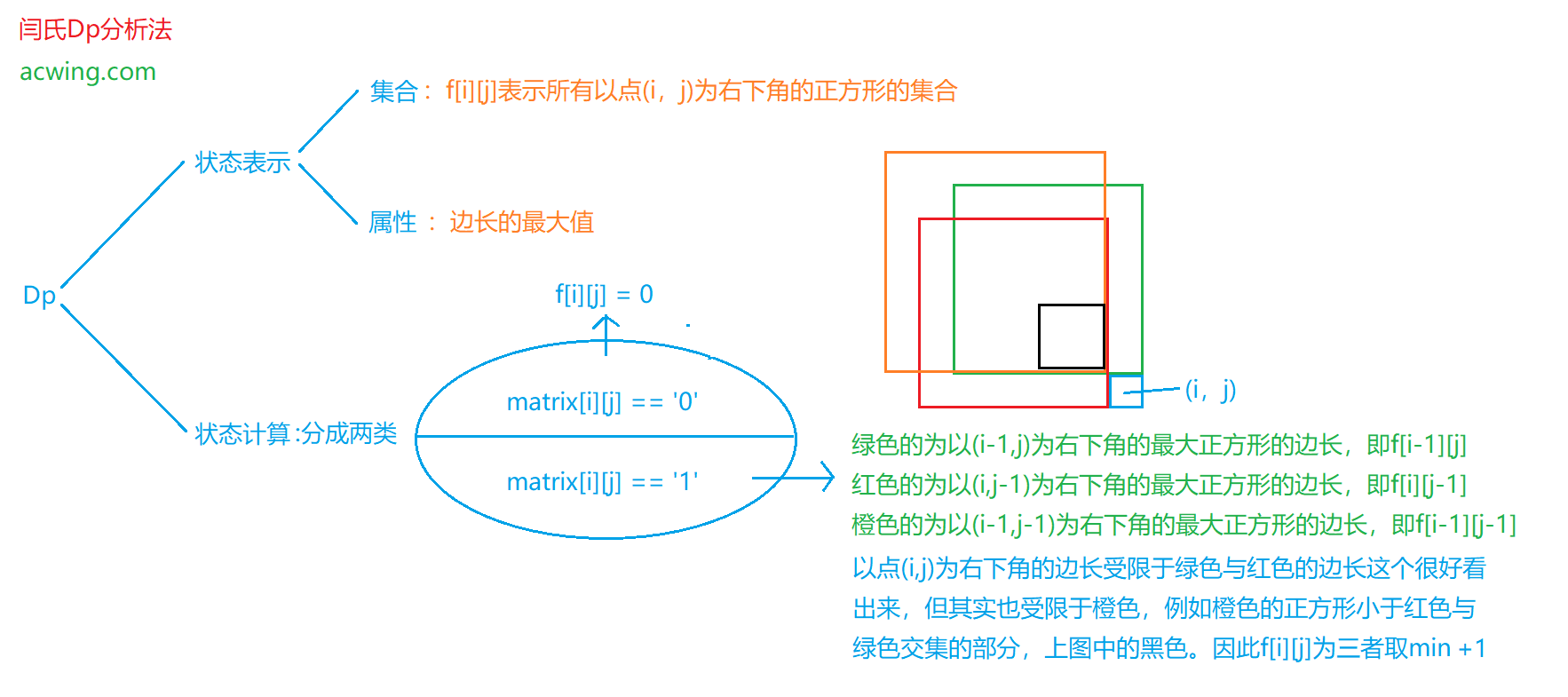
动态规划 时间复杂度：$O(nm)$

代码

因为在计算过程出现了下标减一:f[i-1][j],f[i][j-1],f[i-1][j-1]，为了减少边界的处理，在计算时将横坐标与纵坐标+1

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length;
        if (n == 0) return 0;
        int m = matrix[0].length;
        int[][] f = new int[n + 1][m + 1];
        int ans = 0;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++) {
                int u = i + 1, v = j + 1;
                if (matrix[i][j] == '0') f[u][v] = 0;
                else {
                    f[u][v] = Math.min(f[u - 1][v - 1], Math.min(f[u - 1][v], f[u][v - 1])) + 1;
                    ans = Math.max(ans, f[u][v]);
                }
            }
        return ans * ans;
    }
}