题目描述

给你一棵有 n 个结点的无向树，结点编号为 0 到 n-1，它们中有一些节点有苹果。通过树上的一条边，需要花费 1 秒钟。

你从 结点 0 出发，请你返回最少需要多少秒，可以收集到所有苹果，并回到结点 0。

无向树的边由 edges 给出，其中 edges[i] = [from_i, to_i]，表示有一条边连接 from_i 和 to_i。

除此以外，还有一个布尔数组 hasApple，其中 hasApple[i] = true 代表结点 i 有一个苹果，否则，结点 i 没有苹果。

样例

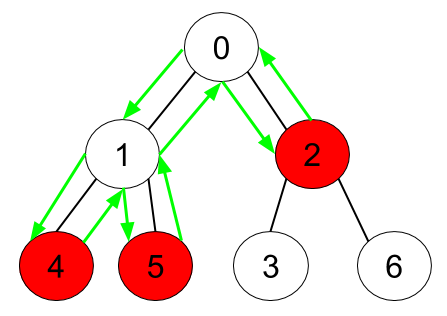
输入：
n = 7,
edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]],
hasApple = [false,false,true,false,true,true,false]
输出：8 
解释：上图展示了给定的树，其中红色结点表示有苹果。
一个能收集到所有苹果的最优方案由绿色箭头表示。

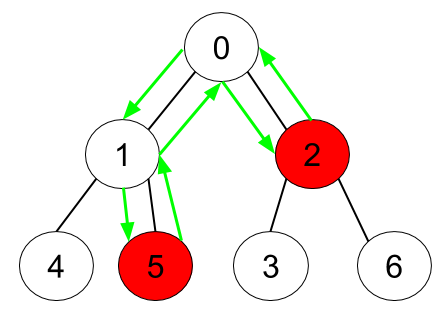
输入：
n = 7,
edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]],
hasApple = [false,false,true,false,false,true,false]
输出：6
解释：上图展示了给定的树，其中红色结点表示有苹果。
一个能收集到所有苹果的最优方案由绿色箭头表示。

输入：
n = 7,
edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]],
hasApple = [false,false,false,false,false,false,false]
输出：0

限制

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= from_i, to_i <= n-1
• from_i < to_i
• hasApple.length == n

算法

(递归遍历) $O(n)$

1. 根据边集数组建立邻接表。
2. 定义布尔型递归函数 solve，计算且该点即将从先序遍历返回时需要的总时间，并返回以该点为根的子树是否存在苹果。
3. 遍历当前点的所有儿子结点，如果某个儿子结点的返回值为 true，则证明这个子树有苹果，且答案需要增加 2 秒，因为需要从当前结点到该儿子结点以及从该儿子结点返回。

时间复杂度

• 每个结点仅遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的空间存储邻接表和系统栈。

C++ 代码

class Solution {
public:
    vector<vector<int>> tree;

    bool solve(int u, int fa, vector<bool> &hasApple, int &ans) {
        for (int v : tree[u])
            if (v != fa) {
                if (solve(v, u, hasApple, ans)) {
                    hasApple[u] = true;
                    ans += 2;
                }
            }

        return hasApple[u];
    }

    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        tree.resize(n);

        for (const auto &e : edges) {
            tree[e[0]].push_back(e[1]);
            tree[e[1]].push_back(e[0]);
        }

        int ans = 0;
        solve(0, -1, hasApple, ans);

        return ans;
    }
};