题目描述

给定一个 rows x cols 大小的矩形披萨和一个整数 k，矩形包含两种字符：'A' （表示苹果）和 '.'（表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

样例

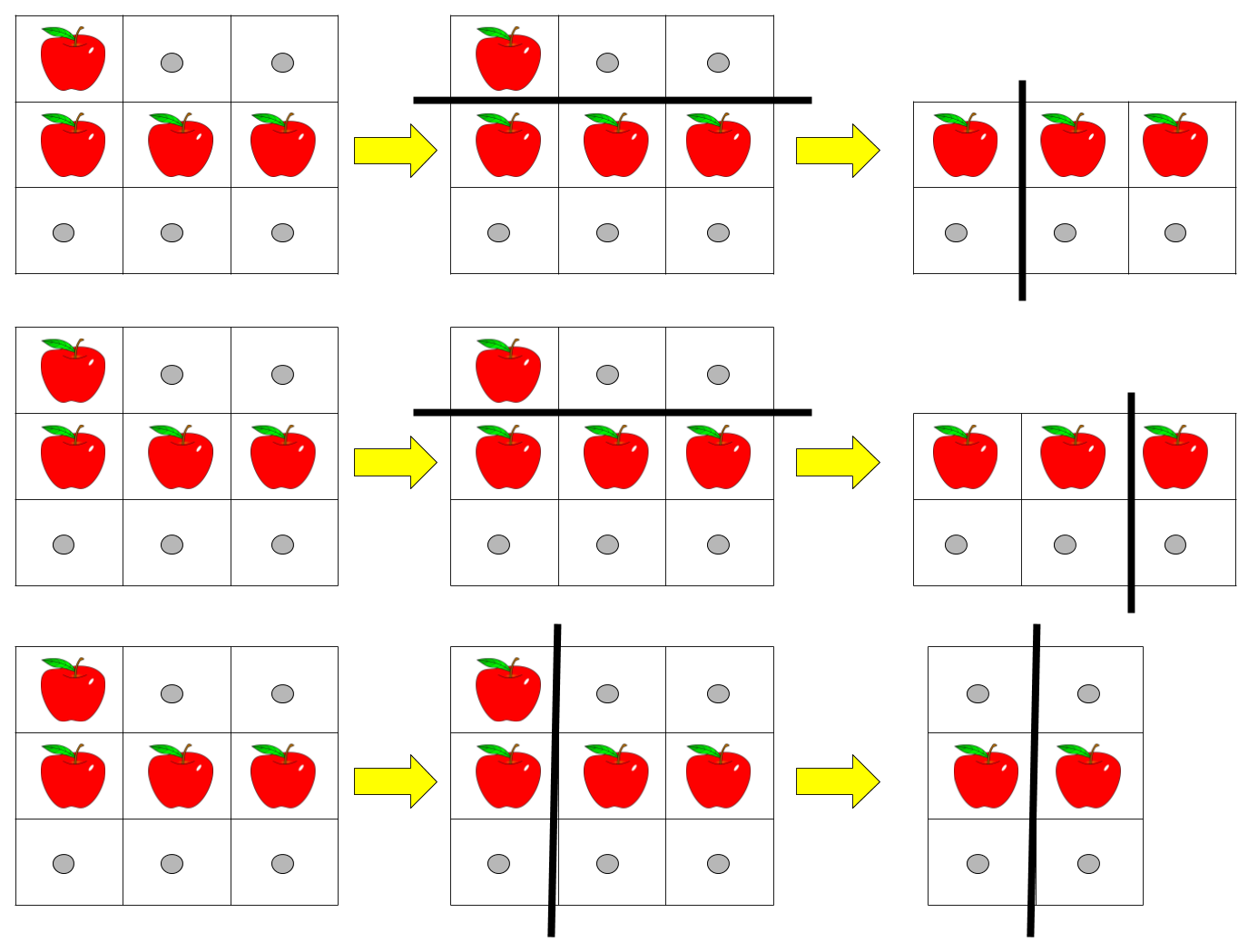
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

输入：pizza = ["A..","AA.","..."], k = 3
输出：1

输入：pizza = ["A..","A..","..."], k = 1
输出：1

限制

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza 只包含字符 'A' 和 '.'。

算法

(动态规划) $O(krc(r + c))$

1. 以左上角为坐标 $[0, 0]$，行为第一维，列为第二维。设 $f(l, i, j)$ 表示将 $[i, j] \times [r - 1, c - 1]$ 右下角的披萨，切 $l$ 刀的合法方案数。
2. 初始时，$f(0, i, j) = check(i, j, r - 1, c - 1)$，其余为 0。
3. 转移时，枚举 $t_i \in [i + 1, r - 1]$，表示当前这一刀是水平切开了 $[i, j] \times [t_i - 1, c - 1]$ 和 $[t_i, j] \times [r - 1, c - 1]$ 这两块，检查 $[i, j] \times [t_i - 1, c - 1]$ 是否存在至少一个苹果，然后转移 $f(l, i, j) = f(l, i, j) + f(l - 1, t_i, j)$。
4. 同理，可以枚举 $t_j \in [j + 1, c - 1]$，检查后，转移 $f(l, i, j) = f(l, i, j) + f(l - 1, i, t_j)$。
5. 最终答案为 $f(k - 1, 0, 0)$。
6. 检查子矩阵是否存在苹果，可以通过后缀和预处理，然后在常数时间内判断。

时间复杂度

• 预处理后缀和时间复杂度为 $O(rc)$。
• 状态数为 $O(krc)$，转移数为 $O(r + c)$，故总时间复杂度为 $O(krc(r+c))$。

空间复杂度

• 需要额外 $O(krc)$ 的空间存储后缀和数组和状态。
• 可以通过滚动数组优化到 $O(rc)$。

C++ 代码

class Solution {
public:
    bool check(int x1, int y1, int x2, int y2, const vector<vector<int>>& p) {
        return p[x1][y1] - p[x2 + 1][y1] - p[x1][y2 + 1] + p[x2 + 1][y2 + 1] > 0;
    }

    int ways(vector<string>& pizza, int k) {
        const int mod = 1000000007;

        int r = pizza.size();
        int c = pizza[0].size();

        vector<vector<vector<int>>> f(k, vector<vector<int>>(r, vector<int>(c, 0)));
        vector<vector<int>> p(r + 1, vector<int>(c + 1, 0));

        for (int i = r - 1; i >= 0; i--)
            for (int j = c - 1; j >= 0; j--)
                p[i][j] = (int)(pizza[i][j] == 'A')
                    + p[i + 1][j] + p[i][j + 1] - p[i + 1][j + 1];

        for (int i = 0; i < r; i++)
            for (int j = 0; j < c; j++)
                f[0][i][j] = (int)(p[i][j] > 0);

        for (int l = 1; l < k; l++)
            for (int i = 0; i < r; i++)
                for (int j = 0; j < c; j++) {
                    for (int ti = i + 1; ti < r; ti++)
                        if (check(i, j, ti - 1, c - 1, p))
                            f[l][i][j] = (f[l][i][j] + f[l - 1][ti][j]) % mod;

                    for (int tj = j + 1; tj < c; tj++)
                        if (check(i, j, r - 1, tj - 1, p))
                            f[l][i][j] = (f[l][i][j] + f[l - 1][i][tj]) % mod;
                }

        return f[k - 1][0][0];
    }
};