题目描述

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts.

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

样例

Example 1:

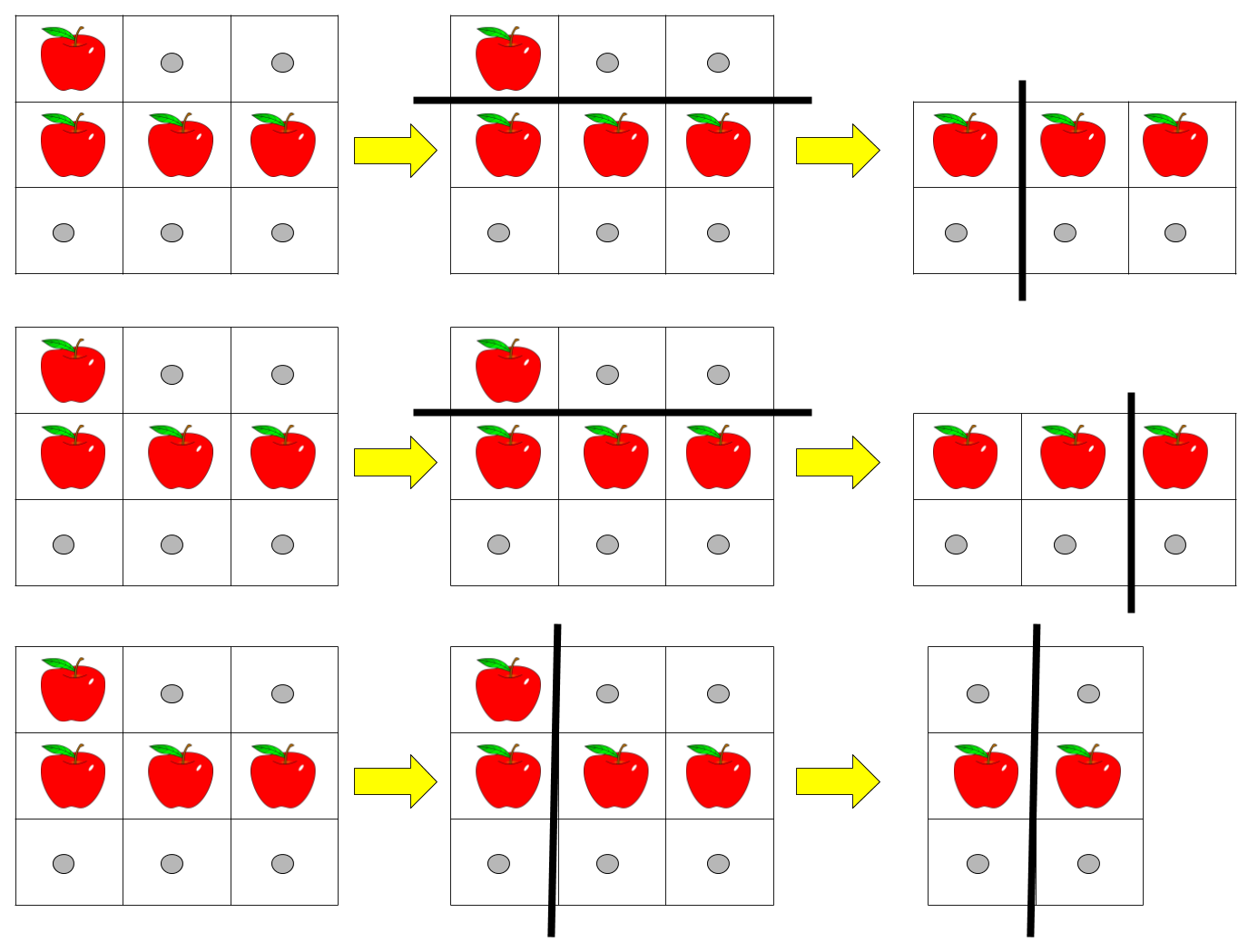
Input: pizza = ["A..","AAA","..."], k = 3
Output: 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

Input: pizza = ["A..","AA.","..."], k = 3
Output: 1

Example 3:

Input: pizza = ["A..","A..","..."], k = 1
Output: 1

Constraints:

• 1 <= rows, cols <= 50
• rows == pizza.length
• cols == pizza[i].length
• 1 <= k <= 10
• pizza consists of characters 'A' and '.' only.

无论横切还是竖切，每次都需要统计右下角剩余部分的苹果数，所以需要进行预处理，用二维数组appleNum记录左上角的苹果数，询问右下角的苹果数时通过函数calculate$O(1)$得到。如果对于这种方法有疑问，可以通过LeetCode 304.Range Sum Query 2D - Immutable体会。

深搜遍历所有可能的切割方案，用数组d[i][j][k]表示从右下角向上i行，向前j列，切成k块的方案数。初始化为-1，如果搜索中发现d[i][j][k]不为-1，代表此种情况已经计算过了。

C++ 代码

class Solution {
    vector<vector<int>> appleNum;
    static const int MODE = 1e9 + 7;
    vector<vector<vector<int>>> d;
    int m, n; //行数和列数


public:
    int ways(vector<string>& pizza, int k) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        appleNum.resize(55, vector<int>(55, 0));
        d.resize(55, vector<vector<int>>(55, vector<int>(15, -1)));
        m = pizza.size(), n = pizza[0].size();
        prePorcess(pizza);

        return DFS(m, n, k);
    }

    //预处理计算当前点到矩阵左上角的苹果数量
    void prePorcess(vector<string>& pizza)
    {
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                appleNum[i][j] = appleNum[i - 1][j] + appleNum[i][j - 1] - appleNum[i - 1][j - 1];
                if (pizza[i - 1][j - 1] == 'A') ++appleNum[i][j];
            }
        }
    }

    //计算从右下角向上rowNum行，向前colNum列的苹果数量
    inline int calculate(int rowNum, int colNum)
    {
        return appleNum[m][n] - appleNum[m - rowNum][n] - appleNum[m][n - colNum] + appleNum[m - rowNum][n - colNum];
    }

    //深搜右下角向上rowNum行，向前colNum列，分成k份的方案数
    int DFS(int rowNum, int colNum, int k)
    {
        //如果剩余的情况已经计算过了
        if (d[rowNum][colNum][k] != -1) return d[rowNum][colNum][k];

        //计算右下角剩余的苹果数
        int cnt = calculate(rowNum, colNum);
        //剩余苹果不够k个，无法继续划分
        if (cnt < k) return d[rowNum][colNum][k] = 0;
        //剩余部分划分成1份，只有一种方案
        if (k == 1) return d[rowNum][colNum][k] = 1;

        d[rowNum][colNum][k] = 0;
        //横着切
        for (int i = 1; i < rowNum; ++i) {
            //必须保证切分的上半部分有苹果
            if (cnt == calculate(rowNum - i, colNum)) continue;
            d[rowNum][colNum][k] = (d[rowNum][colNum][k] + DFS(rowNum - i, colNum, k - 1)) % MODE;
        }

        //竖着切
        for (int i = 1; i < colNum; ++i) {
            //必须保证切分的左半部分有苹果
            if (cnt == calculate(rowNum, colNum - i)) continue;
            d[rowNum][colNum][k] = (d[rowNum][colNum][k] + DFS(rowNum, colNum - i, k - 1)) % MODE;
        }

        return d[rowNum][colNum][k];
    }
};