题目描述

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend in order to collect all apples in the tree starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting the vertices fromi and toi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.

样例

Example 1:

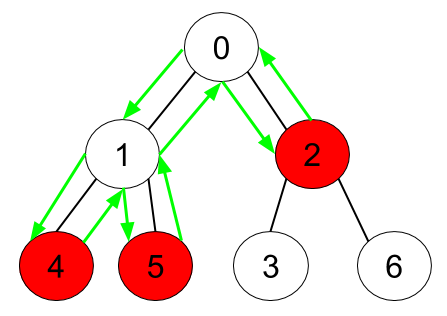
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

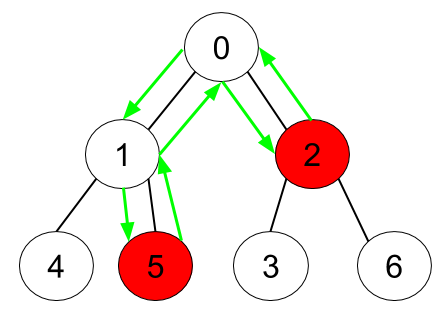
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= fromi, toi <= n-1
• fromi < toi
• hasApple.length == n

用一个哈希表记录从与from节点直接相连的to节点。函数DFS用来计算从startPoint开始采摘苹果所需的时间。

某个节点影响最终结果存在两种情况，一种是在叶节点，一种是出现在中间节点。叶节点比较容易判断，因为用used来记录节点是否被访问过，与叶节点相连的节点肯定都被标记了，所以影响结果的是其hasApple的标记。

中间节点的影响，如果其子节点存在苹果，那么DFS的结果肯定不为0，意味着无论当前节点的标记是什么，都要被访问；如果当前节点的子节点没有苹果，那么当前节点是否被访问取决于其本身是否被标记。一来一回，所以不光要加上tmp的值，还要加2.

时间复杂度$O(n)$。

C++ 代码

class Solution {
    unordered_map<int, vector<int>> um;
    vector<bool> used;
public:
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        used.resize(n, false);
        for (auto & e : edges) {
            int from = e[0], to = e[1];
            um[from].push_back(to);
            um[to].push_back(from);
        }

        return DFS(0, hasApple);
    }

    int DFS(int startPoint, vector<bool>& hasApple)
    {
        int res = 0;
        used[startPoint] = true;

        for (auto & e : um[startPoint]) {
            if (!used[e]) {
                int tmp = DFS(e, hasApple);
                if (tmp || (tmp == 0 && hasApple[e])) res += 2 + tmp;
            }
        }

        return res;
    }
};