题目

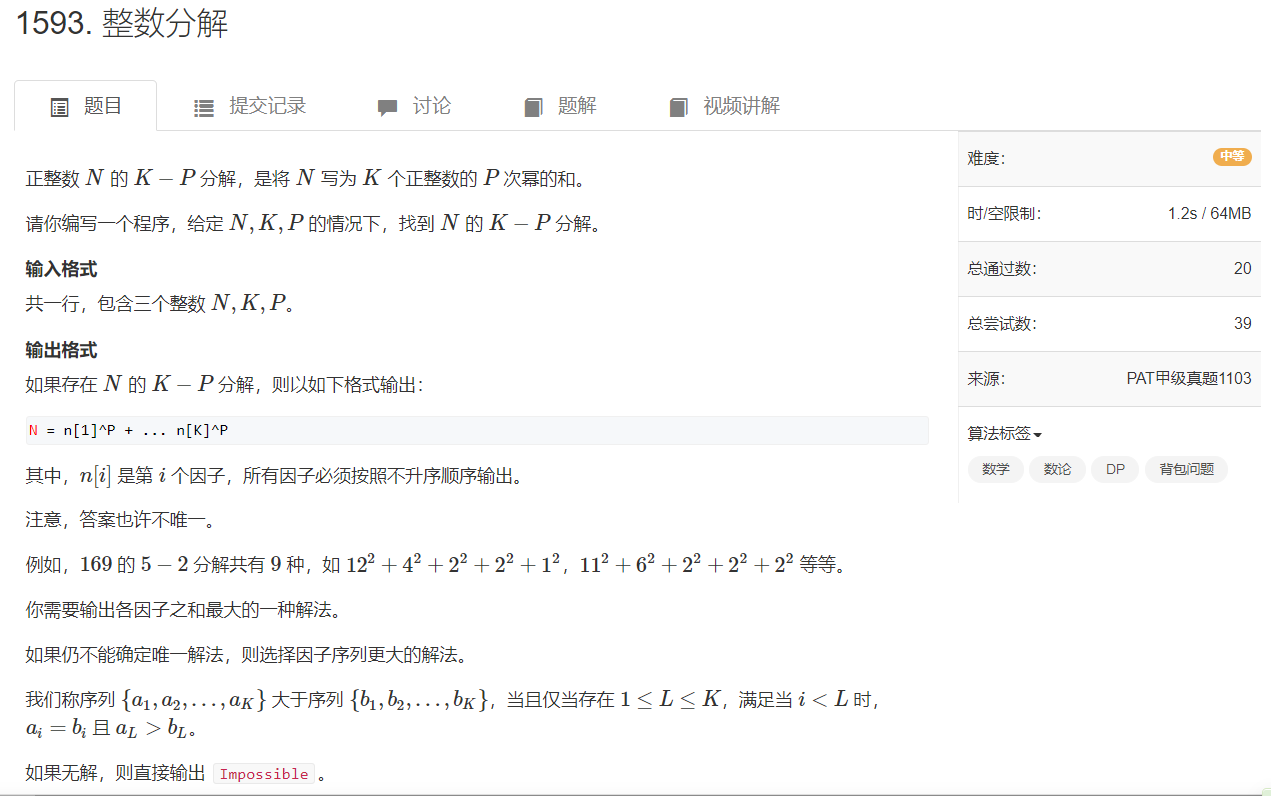
输入输出

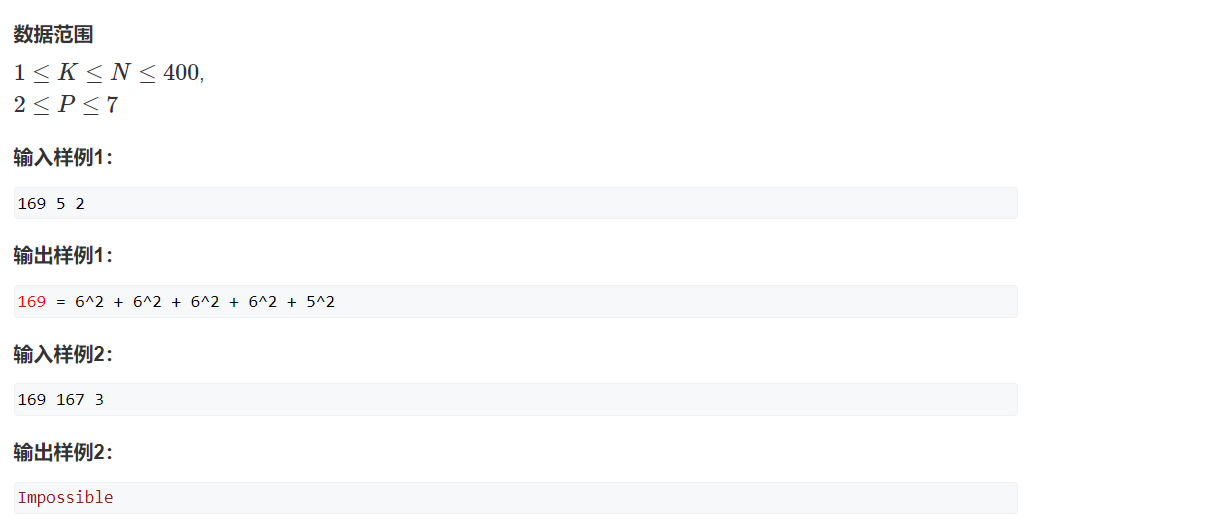
分析

这道题目大致的题意就是给你一个数n，看能不能划分成k个p进制数的和
即划分成n = a1 ^ p + a2 ^ p + … + ak ^ p

这题用暴搜在AcWing上会超时
但是经过昨晚y总的讲解我原来豁然开朗，原来这道题可以转化为一个二维费用的完全背包问题求具体方案问题
这波啊,这波是我没想到的

于是我顺便来整理下大致的思路吧
大致的思路就是把n这个数看成背包的容积N
因为n最多不超过400，然而p进制最少为2
所以物品的价值最大可以取到20(因为20^2 = 400)

时间复杂度20*400*400 = 3200000 < 10^7所以可以用dp来进行求解

每个物品i的体积为i^p,重量为1，价值为i

所以这道题目就被转化成
从前i个物品中取，体积恰好为j，重量恰好为k的取法的方案的最大价值
所以根据闫氏dp分析法我们可以很容易的得到状态转移的方程
f[i][j][k] = max(f[i-1][j][k],f[i][j - v[i]][k - w[i]] + value[i]);

注意点

1. 因为我们要使划分的数恰好分成几个数的和，所以我们就不能像原来那样的背包问题一样设置成体积最多为j和重量最多为k的取法的方案
   定义为体积和重量分别恰好为j和k的时候，我们只用对f[i][j][k]中的值全部memset为负无穷即可
   只定义f[0][0][0] = 0即可
   这样也很好理解，因为根据定义出发体积恰好为j，重量恰好为k的时候
   当i = 0即一件物品都不取的时候，这个时候只有j = k = 0的时候是合法的状态
   即一件不取的时候价值为0，f[0][0][0] = 0
   你如果一件都没取，j和k肯定只能为0，j和k如果不为0，只可能是你取了物品
   但是你没取物品，说明这个状态是不合法的，所以我们就要全部设置为负无穷
   不让后面状态转移从这些不合法的状态转移过来

2. 因为题目要求我们输出各因子之和最大的一种解法
   所以我们就可以把每件物品的价值定义成各个数本身
   即第i个物品的价值为i，这样，我们最后dp得到的最大值就是各因子之和最大的方案

3. 求具体的方案
   因为题目也要求是选择因子序列最大的方案
   所以我们在最后求得最大的价值的时候，我们从最后一个状态转移回去，看能转移到那些状态对应的数，就可以保证我们最后得到的序列的字典序最大
   因为我们是从前往后枚举的，我们最后从后往前枚举能够转移的状态，本身就是从尽可能大的数来开始枚举的，所以最后这样的状态转移可以保证我们得到的序列是字典序最大的
   其次就是我们在求具体的方案的时候，应该用while循环来进行判断状态是否能转移，因为是完全背包，物品的数量是无限的，一个物品可能会被取到多次

4. 什么时候是不存在方案的？
   当f[t][n][k]是小于0的时候，说明我们想要得到的状态是从负无穷即不合法的状态转移过来的，这个时候我们就可以确定是没有解决方案的，直接输出impossible即可

5. 确定物品的个数
   我们可以预先从1开始处理出物品的体积、重量、价值
   第i个物品的体积为i^p,重量为1，价值为i
   且当i^p > n的时候就可以结束循环了，这样子我们就可以确定最多有几个可能取到的物品了

6. 因为PAT的蛋疼的输出，我们需要先定义一个is_first的布尔变量来对第一个进行特别的输出

如果对完全背包问题不太熟悉的话可以看看 3. 完全背包问题
如果对背包问题求具体方案不太熟悉的话可以看看 12. 背包问题求具体方案
如果对二维费用的背包问题不太熟悉的话可以看看 8. 二维费用的背包问题

觉得我贴心的话记得给我点个赞哦~

代码如下

#include <iostream>
#include <cmath>
#include <cstring>

using namespace std;

/*
背包容量为N，重量不超过k
每个物品i从1到20中选，每个物品i对应的体积为i^p，重量为1，价值为i
设f[i][j][k]为从前i个物品中选，体积恰好为j重量恰好为k的最大价值的方案
f[21][410][410]
*/
const int N = 22,M = 410;
int f[N][M][M];
int n,k,p;
int v[N],w[N],value[N];//v[i]和w[i]分别对应第i个物品的体积和重量

int main()
{
    cin>>n>>k>>p;
    memset(f,-0x3f,sizeof f);
    f[0][0][0] = 0;
    int t = 0;
    //自己手动计算出物品对应的体积、重量、价值
    for(int i = 1;i <= 20;i++)
    {
        if(pow(i,p) > n) break;
        v[i] = pow(i,p);
        w[i] = 1;
        value[i] = i;
        t++;
    }
    int i,j,m;
    for(i = 1;i <= t;i++)
        for(j = 0;j <= n;j++)
           for(m = 0;m <= k;m++)
           {
               f[i][j][m] = f[i-1][j][m];
               //跟完全背包一样的推导公式，只不过多了一维
               if(j - v[i] >= 0 && m - w[i] >= 0)f[i][j][m] = max(f[i][j][m],f[i][j - v[i]][m - w[i]] + value[i]);
           }
    int flag = 0;
    bool is_first = true;

    if(f[t][n][k] < 0) puts("Impossible");//如果状态小于0，说明状态不合法，即没有能够成立的方案
    else
    {
        for(i = t,j = n,m = k;i && j && m;i--)
        {
            //如果状态能够转移过来，那么就输出
            while(f[i][j][m] == f[i][j - v[i]][m - w[i]] + value[i])
            {
                if(is_first)
                {
                   cout<<n<<" = "<<i<<"^"<<p;
                   is_first = false;
                }
                else
                {
                   cout<<" + "<<i<<"^"<<p; 
                }

                j -=v[i],m-=w[i];
            }
        }
    }

    return 0;
}