树形DP框架，在框架内部，只需要考虑两层的关系：根+子树，用递归的思路来考虑
区别于线性DP， 将前i项（线性）换成以所有以i为根的子树中的所有物品
每一棵子树：选不选，怎么选 –> 在这样的枚举情况下来取最大值

每一棵子树内部的划分方法：以体积来划分（因为如果用子树中的节点来划分的话，存不下）

如果子树中有k个点，最坏情况下，划分为2^k级别的方案数，若按照体积来划分，那么情况有m种，0~m-1

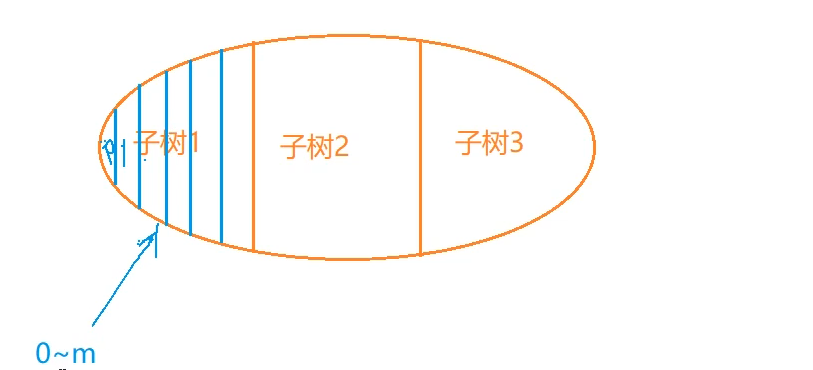
相当于分组背包问题，将每个子树看成一个物品组，从m种方案中选一个出来
因此，按照分组背包的方式循环一遍就可以了

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 110;

int f[N][N];
int v[N], w[N];
int root, n, m;
int h[N], e[N], ne[N], idx;

void add(int a, int b)
{
    e[++ idx] = b, ne[idx] = h[a], h[a] = idx;
}

void dfs(int u)
{
    for (int i = h[u]; i ; i = ne[i]) // 循环每一个组（子树）
    {
        int son = e[i];
        dfs(son); // 把每个组的方案处理好

        for (int j = m - v[u]; j >= 0; j --) // 循环体积
            for (int k = 0; k <= j; k ++) // 循环方案， 方案按照体积分类
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }

    for (int i = m; i >= 0; i --) // 把根节点加入，注意要倒序更新
    {
        if(i >= v[u]) f[u][i] = f[u][i - v[u]] + w[u];
        else f[u][i] = 0;
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
    {
        int p;
        scanf("%d%d%d", v + i, w + i, &p);
        if(p == -1){
            root = i;
            continue;
        }
        add(p, i);
    }

    dfs(root);

    cout << f[root][m] << endl;
}