题目描述

我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

样例

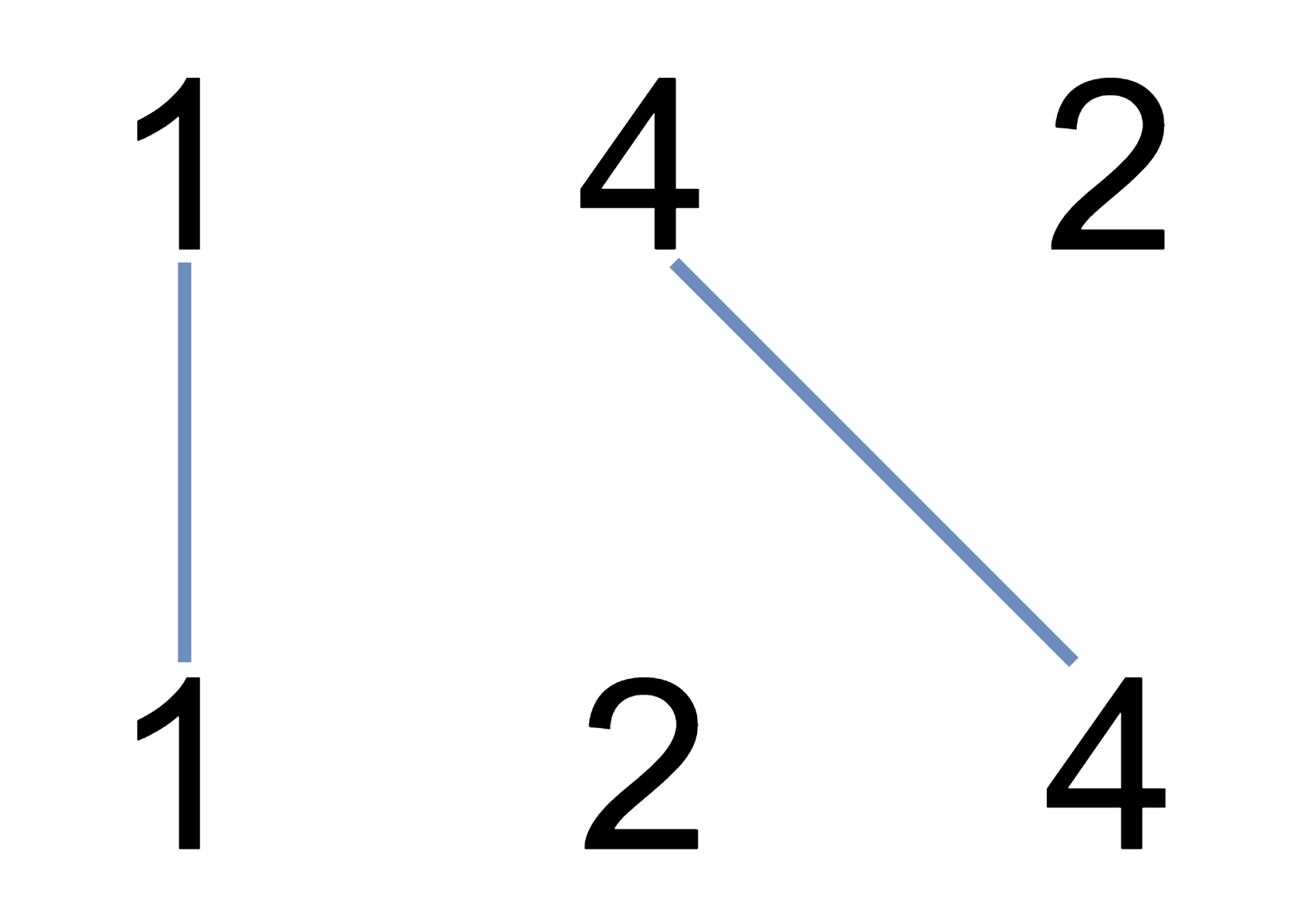
输入：A = [1,4,2], B = [1,2,4]
输出：2
解释：
我们可以画出两条不交叉的线，如上图所示。
我们无法画出第三条不相交的直线，因为从 A[1]=4 到 B[2]=4 的直线将与从 A[2]=2 到 B[1]=2 的直线相交。

输入：A = [2,5,1,2,5], B = [10,5,2,1,5,2]
输出：3

输入：A = [1,3,7,1,7,5], B = [1,9,2,5,1]
输出：2

限制

• 1 <= A.length <= 500
• 1 <= B.length <= 500
• 1 <= A[i], B[i] <= 2000

算法

(动态规划) $O(nm)$

1. 这个问题可以转换为最长公共子序列问题。
2. 设 $f(i, j)$ 表示考虑了 A 的前 i 个数字和 B 的前 j 个数字，所能得到的最大连线数。这里的有效下标从 1 开始。
3. 初始时 f(i, 0) = f(0, j) = 0，其余待定。
4. 转移时，如果 A[i] == B[j]，则 $f(i, j) = f(i - 1, j - 1) + 1$ 表示连一条线。否则 $f(i, j) = \max(f(i - 1, j), f(i, j - 1))$。
5. 最终答案为 $f(n, m)$。

时间复杂度

• 状态数为 $O(nm)$，转移时间为常数，故总时间复杂度为 $O(nm)$。

空间复杂度

• 需要额外 $O(nm)$ 的额外空间存储状态。
• 可以通过滚动数组优化到 $O(m)$。

C++ 代码

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        int n = A.size(), m = B.size();
        vector<vector<int>> f(2, vector<int>(m + 1));

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) {
                if (A[i - 1] == B[j - 1])
                    f[i & 1][j] = f[(i - 1) & 1][j - 1] + 1;
                else
                    f[i & 1][j] = max(f[(i - 1) & 1][j], f[i & 1][j - 1]);
            }

        return f[n & 1][m];
    }
};