原题传送门
题意是有Q个区间询问,每次询问只能得到区间内未被覆盖的位置。
要求一种顺序,使得这Q个询问里的最小值最大。
必须首先发现:最后一个人所得到的座位数量,和前面Q-1个询问的顺序是没有关系的。
所以可以得到一个贪心策略:
1. 从最后一个人开始,枚举谁能得到最多的座位。假设是第X个询问。
2. 去掉第X个询问,再重复步骤一。
3. 重复以上步骤直到询问为空。从得到的答案里取一个最小值即是答案。
如果每一步都暴力枚举,离散化以后复杂度是$O(Q^2)$的(排序以后扫描)。
可以建立一颗长度为N的线段树,线段树上每个点存储当前区间被哪些询问完全覆盖,和区间内点的最少覆盖次数。
考虑到执行覆盖和撤销覆盖的操作都是成对出现的,当前线段被哪些区间完全覆盖可以不用下传懒标记,参考 亚特兰蒂斯 的做法。在往下走的时候,仅仅对第一次遇见的区间进行标记,撤销的时候也无需往下走。
以样例来解释,仅需要在这些有颜色的区间上记录有哪些线段对其进行了覆盖即可。
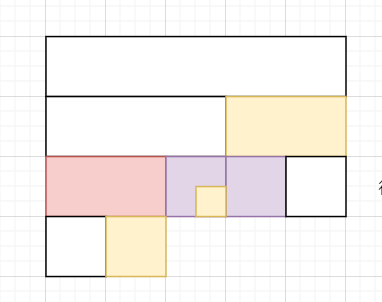
区间最小值就用普通的懒标记,优化到每次修改是$NlogN$。
对于每次找答案,在线段树中往下走找到那些数值为1的点,同时把值赋成无穷大,以后不再访问这个点,在往上回溯的时候在那些只有一个线段覆盖的区间加上这些1的个数。
然后取得值最多的那个线段执行撤销操作。找到最多的区间这一步可以再用一颗线段树维护。
因为记录区间不需要任何顺序,所以用Hash表即可,STL里的unordered_set就能满足。
总的复杂度就成了$Nlog(N+Q)$
#pragma GCC optimize(2)
#include<cstdio>
#include<algorithm>
#include<unordered_set>
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int maxn = 1e6 + 23;
const int INF = 0x3f3f3f3f;
int n, q;
PII seg[30300];
struct NodeQ {
int l, r;
int v;
}trQ[30300 * 4];
void buildQ(int u, int l, int r)
{
if (l == r) trQ[u] = { l, r, 0 };
else
{
trQ[u] = { l, r, 0 };
int mid = l + r >> 1;
buildQ(u << 1, l, mid), buildQ(u << 1 | 1, mid + 1, r);
}
}
void pushupQ(int u)
{
trQ[u].v = max(trQ[u << 1].v, trQ[u << 1 | 1].v);
}
void modifyQ(int u, int p, int x)
{
if (trQ[u].l == trQ[u].r && trQ[u].r == p) trQ[u].v += x;
else
{
int mid = trQ[u].l + trQ[u].r >> 1;
if (p <= mid) modifyQ(u << 1, p, x);
else modifyQ(u << 1 | 1, p, x);
pushupQ(u);
}
}
int queryQ(int u)
{
if (trQ[u].l == trQ[u].r) return trQ[u].l;
else
{
int mid = trQ[u].l + trQ[u].r >> 1;
if (trQ[u << 1].v == trQ[u].v) return queryQ(u << 1);
else return queryQ(u << 1 | 1);
}
}
int w[maxn];
unordered_set<int> st[maxn * 4];
struct Node {
int l, r;
int val;
int add;
}tr[maxn * 4];
void pushdown(int u)
{
if (tr[u].add == 0) return;
tr[u << 1].val += tr[u].add;
tr[u << 1].add += tr[u].add;
tr[u << 1 | 1].val += tr[u].add;
tr[u << 1 | 1].add += tr[u].add;
tr[u].add = 0;
}
void pushup(int u)
{
tr[u].val = min(tr[u << 1].val, tr[u << 1 | 1].val);
}
void build(int u, int l, int r)
{
if (l == r) tr[u] = { l, r, w[l] ? 0 : INF , 0 };
else
{
tr[u] = { l, r, 0, 0 };
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int v, int i)
{
if (tr[u].l >= l && tr[u].r <= r)
{
tr[u].val += v;
tr[u].add += v;
if (v > 0) st[u].insert(i);
else st[u].erase(i);
}
else
{
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) modify(u << 1, l, r, v, i);
else if (l > mid) modify(u << 1 | 1, l, r, v, i);
else modify(u << 1, l, r, v, i), modify(u << 1 | 1, l, r, v, i);
pushup(u);
}
}
int query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r)
{
return tr[u].val;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else return min(query(u << 1, l, r), query(u << 1 | 1, l, r));
}
}
int query(int u)
{
//cerr << u << tr[u].l << tr[u].r << endl;
if (tr[u].l == tr[u].r)
{
tr[u].val = INF;
if (st[u].size() == 1)
modifyQ(1, *st[u].begin(), 1);
return 1;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
int len = 0;
if (tr[u << 1].val == 1) len += query(u << 1);
if (tr[u << 1 | 1].val == 1) len += query(u << 1 | 1);
if (st[u].size() == 1)
modifyQ(1, *st[u].begin(), len);
pushup(u);
return len;
}
}
int main()
{
int T = 0; scanf("%d", &T);
for (int cas = 1; cas <= T; cas++)
{
scanf("%d%d", &n, &q);
buildQ(1, 1, q);
if(cas != 1)for (int i = 1; i <= q; i++) st[i].clear();
if(cas != 1) memset(w, 0, sizeof w);
for (int i = 1; i <= q; i++)
{
scanf("%d%d", &seg[i].first, &seg[i].second);
//modify(1, seg[i].first, seg[i].second, 1, i);
w[seg[i].first]++; w[seg[i].second + 1]--;
}
for (int i = 1; i <= n; i++) w[i] += w[i - 1];
build(1, 1, n);
for (int i = 1; i <= q; i++) modify(1, seg[i].first, seg[i].second, 1, i);
int ans = 0x3f3f3f3f;
for (int i = 1; i <= q; i++)
{
query(1);
ans = min(ans, trQ[1].v);
int sid = queryQ(1);
modify(1, seg[sid].first, seg[sid].second, -1, sid);
modifyQ(1, sid, -INF);
}
printf("Case #%d: %d\n", cas, ans);
}
}
/*
1
20 5
9 19
2 5
6 6
2 3
8 19
1
20 5
10 19
2 5
6 6
2 3
9 19
3
5 3
1 2
3 4
2 5
30 3
10 11
10 10
11 11
10 4
1 8
4 5
3 6
2 7
*/


six six six