卡特兰数( $C^{n}_{2n} / (n+1)$)

题目：定n个0和n个1，它们将按照某种顺序排成长度为2n的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。

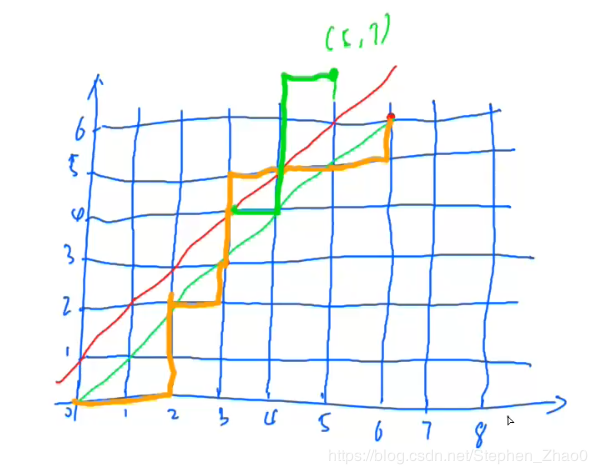
举个栗子：n=6时，就可以画成上图，假设向右是0向上是1，则在红线以下的路径是合法的，可以看出每一条从（0,0）走到（6,6）的非法路径做关于红线的对称，都对应一条（0,0）-（5,7）的路径；反之，每一条从（0,0）-（5,7）的路径都对应一条从（0,0）-（6,6）的非法路径，那么就可以利用（0,0）-（5,7）的路径数间接求出（0,0）-（6,6）的非法路径数。

算法核心：每一条从（0,0）走到（n，n）的非法路径都对应一条从（0,0）走到（n-1,n+1）的非法路径，因此合法路径就是
因此从（0,0）走到（6,6）的不合法路径数就是$C^{n-1} _ {2n}$ , 即合法的是 $C _ {2n}^{n} - C _ {2n}^{n-1}$ ，化简得 $\frac{C_{2n}^n}{n+1}$，
所以直接从定义出发求出$C ^ {n} _ {2n}$ ，其中因为模上一个质数，可以用快速幂求逆元。

C++ 代码

#include <iostream>

using namespace std;

const int mod = 1e9 + 7;

using LL = long long;

int qmi(int a , int b)
{
    int res = 1;
    while(b)
    {
        if(b & 1) res = (LL)res * a % mod;
        b >>= 1;
        a = (LL) a * a % mod;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;

    int res = 1;

    for(int i = 2 * n ; i > n ; i--) res = (LL)res * i % mod;

    for(int i = n ; i ; i --) res = (LL) res * qmi(i , mod - 2) % mod;

    res = (LL) res * qmi(n + 1 , mod - 2) % mod;

    cout << res << endl;
    return 0;
}