用 $D(x)$ 表示买入操作，$F[x]$ 表示卖出操作
那么很显然，要让差价最大
$D(x):= \min(cost(st \rightarrow x))$
$F(x)$ 表示卖出操作，研究对象显然是 $\text{path}:=(x\rightarrow ed)$
如果建一个反图，那么实际上
$F(x):= \max(cost(ed\rightarrow x))$
最后遍历
$\forall x \in G, \ \ \max (F[x] - D[x])$

这个问题可以用 $\text{Dijkstra}$ 解决吗？看状态方程
因为 $D(x)$ 表示从 $st\rightarrow x$ 路径中最小的权值，状态转移如下
$\forall (x,y) \in E(G)$
$\quad \quad D(y) = \min(D(x), c(x,y))$

$\textbf{这里不能用 Dijkstra}$
$D(y) = \min(D(x), price(y))$

假设 $\text{Dijkstra}$ 的优先队列中的 $\min \text{top()}$ 为 $x$
$\text{Dijkstra}$ 循环不变式认为
$\forall (x, …)$
$\quad \quad x \text{ 是当前最小值}$
$\quad \quad \text{之后的遍历只会增大 } D(x)$

来看一个有环图

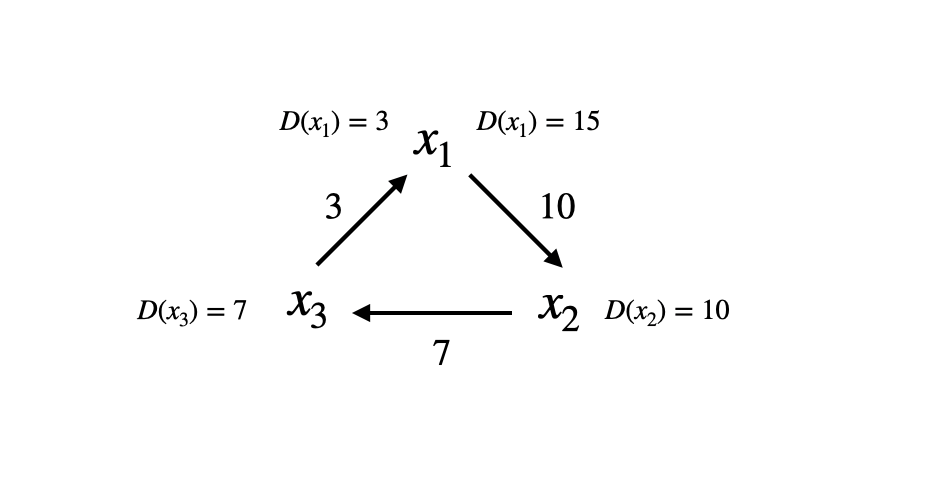
用 $\text{Dijkstra}$ 会得到一个更小的 $D(x_1)$

这里改用 $\textbf{spfa}$

const int maxn = 100000 + 10;
const int inf = 0x3f3f3f3f;
int N, M;
int A[maxn];

// == Graph definition ==
vector<int> G1[maxn];
vector<int> G2[maxn];
class Edge {
public:
    int to;
    Edge() {}
    Edge(int t) : to(t) {}
};
vector<Edge> edges1;
vector<Edge> edges2;

void initG1(int n) {
    _rep(i, 0, n) G1[i].clear();
    edges1.clear();
}

void initG2(int n) {
    _rep(i, 0, n) G2[i].clear();
    edges2.clear();
}

void addEdge1(int u, int v) {
    edges1.push_back(Edge(v));
    G1[u].push_back(edges1.size() - 1);
}

void addEdge2(int u, int v) {
    edges2.push_back(Edge(v));
    G2[u].push_back(edges2.size() - 1);
}
// == Graph definition finished ==

// == dijkstra, D[] used min, F[] used max ==
bool inq[maxn];
int D[maxn], F[maxn];

void initSpfa1() {
    Set(inq, 0);
    Set(D, inf);
    D[1] = A[1];
}

void initSpfa2() {
    Set(inq, 0);
    Set(F, -inf);
    F[N] = A[N];
}


void spfa1() {
    initSpfa1();
    queue<int> que1;
    que1.push(1);
    inq[1] = true;

    while (!que1.empty()) {
        int x = que1.front();
        que1.pop();
        inq[x] = false;

        _for(i, 0, G1[x].size()) {
            int y = edges1[G1[x][i]].to;
            if(D[x] < inf && D[y] > min(D[x], A[y])) {
                D[y] = min(D[x], A[y]);
                if(!inq[y]) {
                    que1.push(y);
                    inq[y] = true;
                }
            }
        }
    }
}

void spfa2() {
    initSpfa2();
    queue<int> que2;
    que2.push(N);
    inq[N] = 1;

    while (!que2.empty()) {
        int x = que2.front();
        que2.pop();
        inq[x] = false;

        _for(i, 0, G2[x].size()) {
            int y = edges2[G2[x][i]].to;
            if(F[x] > -inf && F[y] < max(F[x], A[y])) {
                F[y] = max(F[x], A[y]);
                if(!inq[y]) {
                    que2.push(y);
                    inq[y] = true;
                }
            }
        }
    }
}
// == dijkstra finished ==

int main() {
    freopen("input.txt", "r", stdin);
    cin >> N >> M;
    initG1(N);
    initG2(N);

    // get price data A[]
    _rep(i, 1, N) scanf("%d", &A[i]);

    // build Graph
    _rep(i, 1, M) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        addEdge1(x, y);
        addEdge2(y, x);

        if(z == 2) {
            addEdge1(y, x);
            addEdge2(x, y);
        }
    }

    // dijkstra
    spfa1();
    spfa2();

    int Ans = 0;
    _rep(i, 1, N) Ans = max(Ans, F[i] - D[i]);
    cout << Ans << endl;
}