题目描述

给你一棵根为 root 的二叉树，请你返回二叉树中好结点的数目。

好结点 X 定义为：从根到该结点 X 所经过的结点中，没有任何结点的值大于 X 的值。

样例

输入：root = [3,1,4,3,null,1,5]
输出：4
解释：图中蓝色节点为好结点。
根结点 (3) 永远是个好结点。
结点 4 -> (3,4) 是路径中的最大值。
结点 5 -> (3,4,5) 是路径中的最大值。
结点 3 -> (3,1,3) 是路径中的最大值。

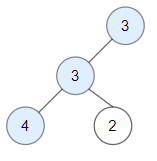
输入：root = [3,3,null,4,2]
输出：3
解释：结点 2 -> (3, 3, 2) 不是好结点，因为 "3" 比它大。

输入：root = [1]
输出：1
解释：根节点是好结点。

限制

• 二叉树中节点数目范围是 [1, 10^5]。
• 每个节点权值的范围是 [-10^4, 10^4]。

算法

(递归遍历) $O(n)$

1. 递归遍历整棵树，遍历过程中，记录从根结点到当前结点的最大值。

时间复杂度

• 每个结点仅遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(h)$ 的空间存储递归系统栈，$h$ 是树的最大高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void solve(TreeNode *rt, int ma, int &ans) {
        if (!rt)
            return;

        if (ma <= rt->val)
            ans++;

        solve(rt->left, max(ma, rt->val), ans);
        solve(rt->right, max(ma, rt->val), ans);
    }

    int goodNodes(TreeNode* root) {
        int ans = 0;
        solve(root, INT_MIN, ans);
        return ans;
    }
};