题目描述

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r。

请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

样例

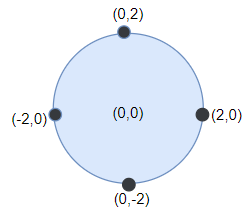
输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0, 0)，半径为 2，
所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4。

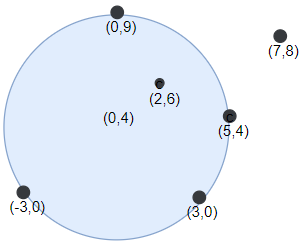
输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0, 4)，半径为 5，
则除了 (7, 8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5。

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1

输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4

限制

• 1 <= points.length <= 100
• points[i].length == 2
• -10^4 <= points[i][0], points[i][1] <= 10^4
• 1 <= r <= 5000

算法

(贪心，暴力枚举) $O(n^3)$

1. 答案的下限为 1。
2. 枚举距离不为 0 且小于等于 2r 的点对 (x1, y1) 和 (x2, y2)，求出两组圆心，满足 (x1, y1) 和 (x2, y2) 恰好在圆周上。
3. 求圆心的过程如下：
   • 求出两个点的中点坐标 (midx, midy)。
   • 求出中点到这两个点的距离 half_d。
   • 求出长度为 r，起点为 (x1, y1)，方向朝向 (x2, y2) 的向量 (vx, vy)。
   • 求出 (x1, y1) 到圆心与其到中点的角的余弦值 cos_t 和正弦值 sin_t。
   • 将向量 (vx, vy) 逆时针旋转 t 和 -t，根据旋转公式，可以得到两组圆心。
4. 枚举所有点，统计有多少点在这两个圆上，更新答案。
5. 算法的正确性很容易证明，如果存在一个最大覆盖的圆且最多仅有一个点在圆周上，则我们可以通过移动这个圆，使得至少两个点到了圆周上，且保证覆盖数不会减少。
6. 注意，最后统计的时候，需要通过添加小量来修正精度误差。

时间复杂度

• 枚举两个点构造两组圆，然后枚举所有点统计，时间复杂度为 $O(n^3)$。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

class Solution {
public:
    const double eps = 1e-8;

    double sqr(double x) {
        return x * x;
    }

    double dis_sqr(double x1, double y1, double x2, double y2) {
        return sqr(x1 - x2) + sqr(y1 - y2);
    }

    double dis(double x1, double y1, double x2, double y2) {
        return sqrt(dis_sqr(x1, y1, x2, y2));
    }

    void center(double x1, double y1, double x2, double y2, double r,
                double &rx1, double &ry1, double &rx2, double &ry2) {

        double midx = (x1 + x2) / 2;
        double midy = (y1 + y2) / 2;
        double half_d = dis(midx, midy, x1, y1);

        double vx = (midx - x1) / half_d * r;
        double vy = (midy - y1) / half_d * r;

        double cos_t = (half_d / r);
        double sin_t = sqrt(1 - sqr(cos_t));

        rx1 = vx * cos_t - vy * sin_t + x1;
        ry1 = vx * sin_t + vy * cos_t + y1;

        rx2 = vx * cos_t + vy * sin_t + x1;
        ry2 = -vx * sin_t + vy * cos_t + y1;
    }

    int check(const vector<vector<int>>& points, double rx, double ry, double r) {
        int n = points.size();
        int cnt = 0;

        for (int k = 0; k < n; k++)
            if (dis(rx, ry, points[k][0], points[k][1]) <= r + eps)
                cnt++;

        return cnt;
    }

    int numPoints(vector<vector<int>>& points, int r) {
        int n = points.size();

        int ans = 1;
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n; j++) {
                double ds = dis_sqr(points[i][0], points[i][1], points[j][0], points[j][1]);
                if (ds == 0 || ds > 4 * sqr(r))
                    continue;

                double rx1, ry1, rx2, ry2;
                center(points[i][0], points[i][1], points[j][0], points[j][1], r,
                       rx1, ry1, rx2, ry2);

                ans = max(ans, check(points, rx1, ry1, r));
                ans = max(ans, check(points, rx2, ry2, r));

                if (ans == n)
                    return ans;
            }

        return ans;
    }
};