题意

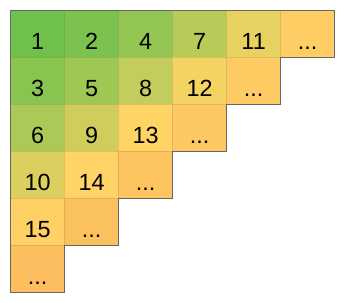
给定一个从右上到左下斜向递增的图形，只能向右和下走。
输入两个坐标：x1,y1,x2,y2。(x1 < x2, y1 < y2)
从 (x1,y1) 走到 (x2,y2) 经过的数字进行求和，问和有多少种。

思路

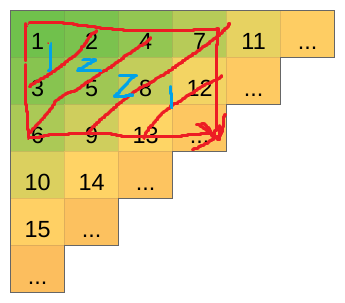
因为每次向右走比向下走少一，所以先向右一直走，再向下走，和为最小。
同理先向下走，再向右走，和最大。将向下走提前一位，和就会加一，所以中间的值都能够取到。
答案就是最大的和 - 最小的和 + 1。

设x为短边，每次向下走比向右走大1，x走到底时，总共相差1+2+...+x-1 = x*(x-1)/2。
中间如果有多出来的部分 数都相差x-1。
最后和第一次对称，也是相差 x*(x-1)/2。
总的格子为x+y-3（去掉了首尾相同的格子）,中间的格子数为(x+y-3) - 2*(x-1) = y-x-1。
所以最大最小和相差(y-x-1) * (x-1) + x*(x-1) = (x-1)*(y-1).答案为:(x-1)*(y-1) + 1.

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 200010;

typedef long long ll;

void solve()
{
    ll x1,y1,x2,y2;
    cin >> x1 >> y1 >> x2 >> y2;
    cout << (x2-x1) * (y2-y1) + 1 << endl;
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t;
    cin >>t;
    while(t--)
    {
        solve();
    }
}