算法思路：每次选择最小的两个点合并即可，利用优先队列（小根堆）

这些点会构成一棵哈夫曼树（完全二叉树）。
.处于深度最深的点会被合并最多次（可以理解为优先合并）。

证明正确性：
先证明以下两点：
①权值最小的两个点，深度一定最深，并且可以互为兄弟（即优先合并，并且局部代价最小）
证明：假设最小的两点深度不是最深，设点a、f是最小的两个点。

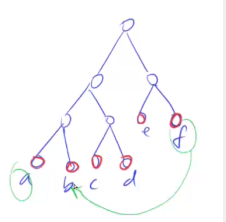
当交换点b和点f后，因为最终的结果等于每个点的大小✖每个点到树根的距离，其余点不变，
因此最终的结果会从3b+2f变成3f+2b，因为f<b所以结果变小。
于是得证：合并最小的两个点是局部最优解

②一定可以通过局部最优解得到全局最优解
证明：
设函数f(x)表示一棵大小为x的哈夫曼树的代价。F(x)表示数大小为x的最小代价
由局部最优解得：f(n) = f(n-1) + a + b
因为不管是哪一种方案，第一步总是要合并a+b，因此先不考虑a+b，只考虑f(n-1)
于是问题变为求f(n-1)的最优解，于是可以再调用局部最优解的方案，以此类推直到n=1。
于是证得：可以通过局部最优解的方式得到全局最优解

C++ 代码

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int main()
{
    int n;
    cin >> n;

    priority_queue<int , vector<int> , greater<int>> heap;

    for(int i = 0 ; i < n ; i++)
    {
        int x;
        cin >> x;
        heap.push(x);
    }

    int res = 0;
    while(heap.size() > 1)
    {
        int x = heap.top();
        heap.pop();
        int y = heap.top();
        heap.pop();
        res += x + y;
        heap.push(x + y);
    }

    cout << res << endl;
    return 0;
}