题目描述

墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。

投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。

请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

样例

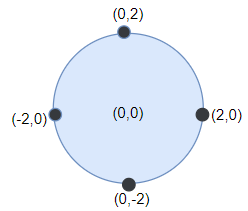
输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出：4
解释：如果圆形的飞镖靶的圆心为 (0,0) ，半径为 2 ，所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为4。

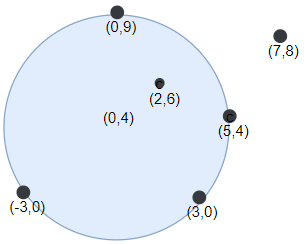
输入：points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出：5
解释：如果圆形的飞镖靶的圆心为 (0,4) ，半径为 5 ，则除了 (7,8) 之外的飞镖都落在靶上，
此时落在靶上的飞镖数最大，值为 5 。

输入：points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
输出：1

输入：points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
输出：4

提示：

• 1 <= points.length <= 100
• points[i].length == 2
• -10^4 <= points[i][0], points[i][1] <= 10^4
• 1 <= r <= 5000

算法分析

枚举

• 1、枚举两两点的组合，已知两个点 $A$ ， $B$ 的坐标，因此圆心在$AB$垂直的平分线上，又已知圆心到的半径，即圆心到 $A$ 和 $B$ 的距离，当$r >= \frac{d}{2}$时一定可以找到经过这两个点 $A$，$B$ 的圆所对应的圆心的坐标
• 2、确定圆心坐标和半径后，通过其他点到圆心的距离是否小于等于半径，判断该圆能覆盖多少个点，更新ans，
• 3、当ans = 0时，表示所有两两点组合都不能构成一个合法圆，因此最多能覆盖的数量一定是1个
• 4、计算圆心坐标
  

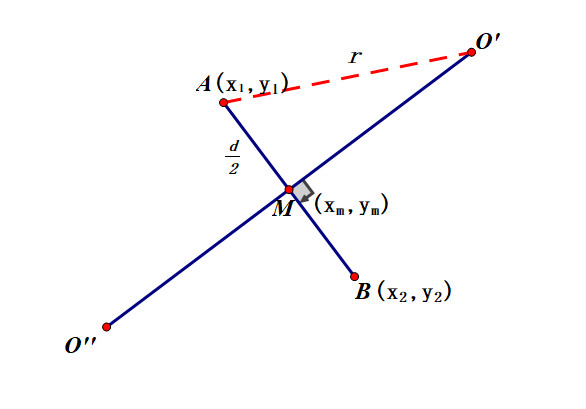
如图所示，$\vec{AB} = (x_{2} - x_{1},y_{2} - y_{1}) = (v_{1},v_{2})$

算出$A$点和$B$点的中点坐标 $M(x_m,y_m) = (\frac{(x_1 + x_2)}{2},\frac{(y_1 + y_2)}{2})$

再算出$AB$的长度 $d = \sqrt{ (x_{1} - x_{2})^2 + (y_{1} - y_{2})^2 }$

因此中点到圆心的距离 $MO^{’}$ 和 $MO^{’’}$是 $len = \sqrt{r^2 - (\frac{d}{2})^2}$

只需要知道中点坐标，中点到圆心的单位向量，中点到圆心的距离，就能求出圆心具体坐标

由于两个向量垂直，向量相乘等于-1，因此可得 $\vec{MO^{’}} = (-v_{2},v_{1})$，$\vec{MO^{’’}} = (v_{2},-v_{1})$

因此$\vec{MO^{’}}$对应的单位向量是 $(- \frac{v_2}{\sqrt{v_1^2 + v_2^2}},\frac{v_1}{\sqrt{v_1^2 + v_2^2}})$，$\vec{MO^{’’}}$对应的单位向量是 $( \frac{v_2}{\sqrt{v_1^2 + v_2^2}},- \frac{v_1}{\sqrt{v_1^2 + v_2^2}})$

因此圆心 $O^{’}$ 坐标是 $(x_{o1},y_{o1}) = (x_m,y_m) + len * (- \frac{v_2}{\sqrt{v_1^2 + v_2^2}},\frac{v_1}{\sqrt{v_1^2 + v_2^2}})$
圆心 $O^{’’}$ 坐标是 $(x_{o2},y_{o2}) = (x_m,y_m) + len * ( \frac{v_2}{\sqrt{v_1^2 + v_2^2}},- \frac{v_1}{\sqrt{v_1^2 + v_2^2}})$

时间复杂度 $O(n^3)$

Java 代码

class Solution {
    public int numPoints(int[][] points, int r) {
        int n = points.length;
        int ans = 0;
        for(int i = 0;i < n;i ++)
        {
            for(int j = i + 1;j < n;j ++)
            {
                //算出两点的距离
                int x1 = points[i][0],y1 = points[i][1];
                int x2 = points[j][0],y2 = points[j][1];
                double d = Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
                if(r < d / 2) continue;

                int v1 = x2 - x1,v2 = y2 - y1;

                //中点坐标
                double xm = (x1 + x2) / 2.0,ym = (y1 + y2) / 2.0;
                //中点到圆心的距离
                double len = Math.sqrt(r * r - (d / 2) * (d / 2));
                //算出两个圆心的坐标
                double xo1 = xm + len * ((-v2) / d),yo1 = ym + len * (v1 / d);
                double xo2 = xm + len * (v2 / d),yo2 = ym + len * ((-v2) / d);
                int res1 = 0;
                for(int k = 0;k < n;k ++)
                {
                    double x = points[k][0],y = points[k][1];
                    if(Math.sqrt((x - xo1) * (x - xo1) + (y - yo1) * (y - yo1)) - r < 1e-8)
                        res1 ++;
                }
                ans = Math.max(ans, res1);

                int res2 = 0;
                for(int k = 0;k < n;k ++)
                {
                    double x = points[k][0],y = points[k][1];
                    if(Math.sqrt((x - xo2) * (x - xo2) + (y - yo2) * (y - yo2)) - r < 1e-8)
                        res2 ++;
                }
                ans = Math.max(ans, res2);

            }
        }
        if(ans == 0) return 1;
        return ans;
    }
}