题目描述

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

样例

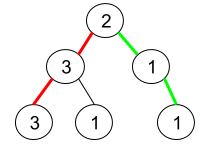
输入：root = [2,3,1,3,1,null,1]
输出：2 
解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：
     红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。
     在这些路径中，只有红色和绿色的路径是伪回文路径，
     因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。

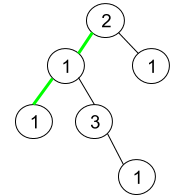
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1 
解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。
     这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。

提示：

• 给定二叉树的节点数目在 1 到 10^5 之间。
• 节点值在 1 到 9 之间。

算法分析

dfs

• dfs从根结点到达每个结点时对应着这条路径的数字s，调用check函数判断该结点对应的路径s是否是伪回文路径，若是则更新全局变量ans ++

时间复杂度 $O(nlogn)$

枚举到每个点复杂度是$O(n)$，最长的路径长度是$logn$，因此判断路径是否是伪回文路径的复杂度是$O(nlogn)$

Java 代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    static int ans = 0;
    static boolean check(String s)
    {
        int[] t = new int[10];
        for(int i = 0;i < s.length();i ++) t[s.charAt(i) - '0'] ++;

        int cnt = 0;
        for(int i = 1;i <= 9;i ++)
            if(t[i] > 0 && t[i] % 2 != 0)
                cnt ++;

        return cnt < 2;
    }
    static void dfs(TreeNode root,String s)
    {
        s += root.val;
        if(root.left == null && root.right == null && check(s)) ans ++;
        if(root.left != null) dfs(root.left,s);
        if(root.right != null) dfs(root.right,s);
    }
    public int pseudoPalindromicPaths (TreeNode root) {
        ans = 0;
        dfs(root,"");
        return ans;
    }
}