对于一张图

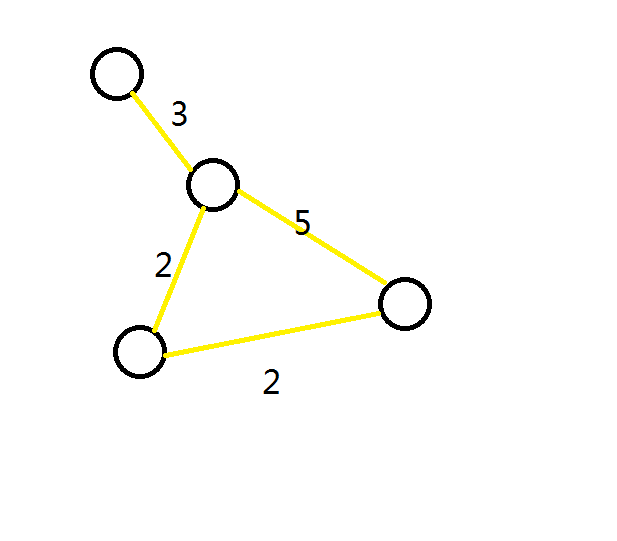
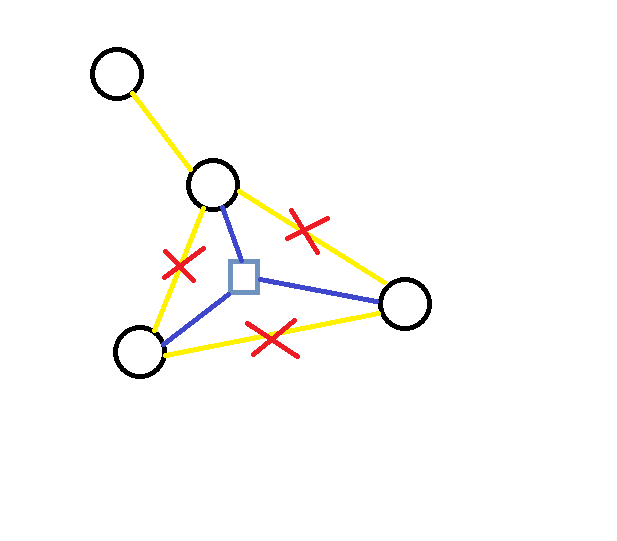
找到环，删去环上边，将环上的节点都连在一个新建点上

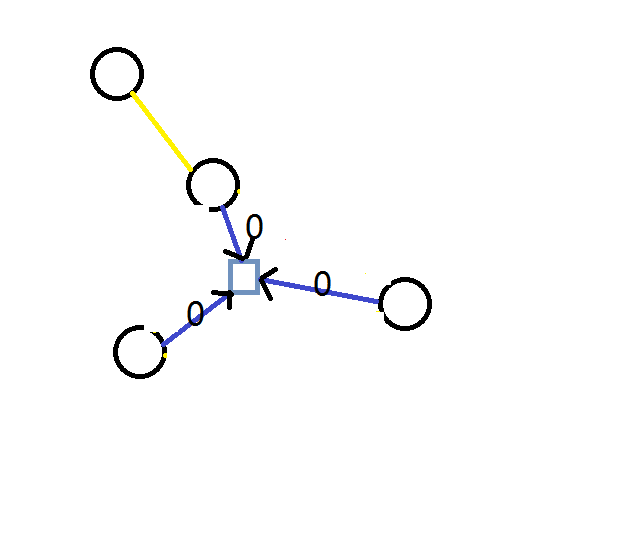
进入新建点的边的边权设为0

离开新建点的边的边权设为离开的点到？(代号)的最短路

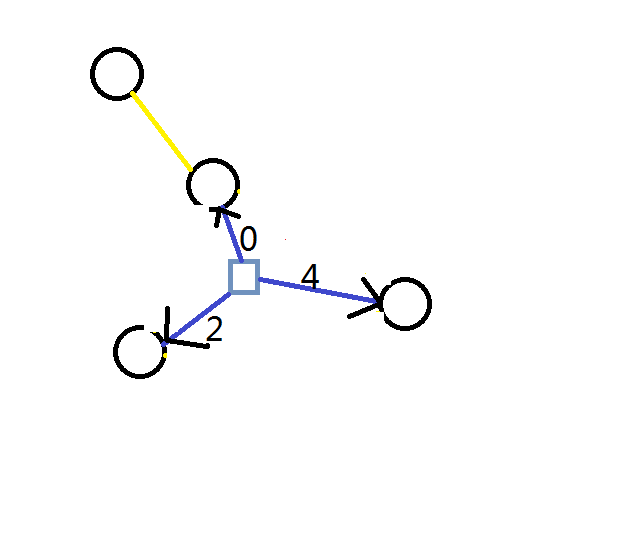
对环上点来说，？(代号)是环上走最少的边就能到根节点的点

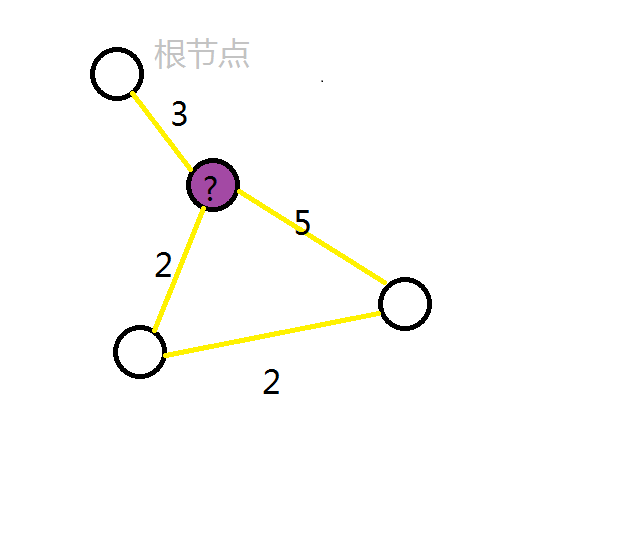
这样就可以当作树来做
但是，还有特殊情况
比如图

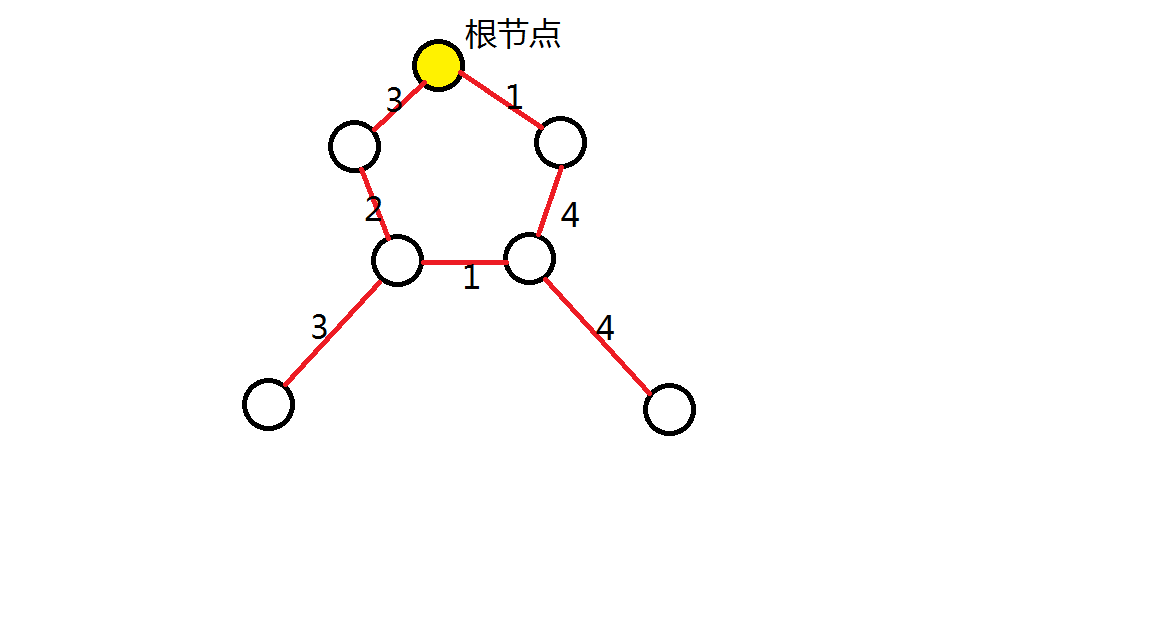
处理后，求x到y的最短路

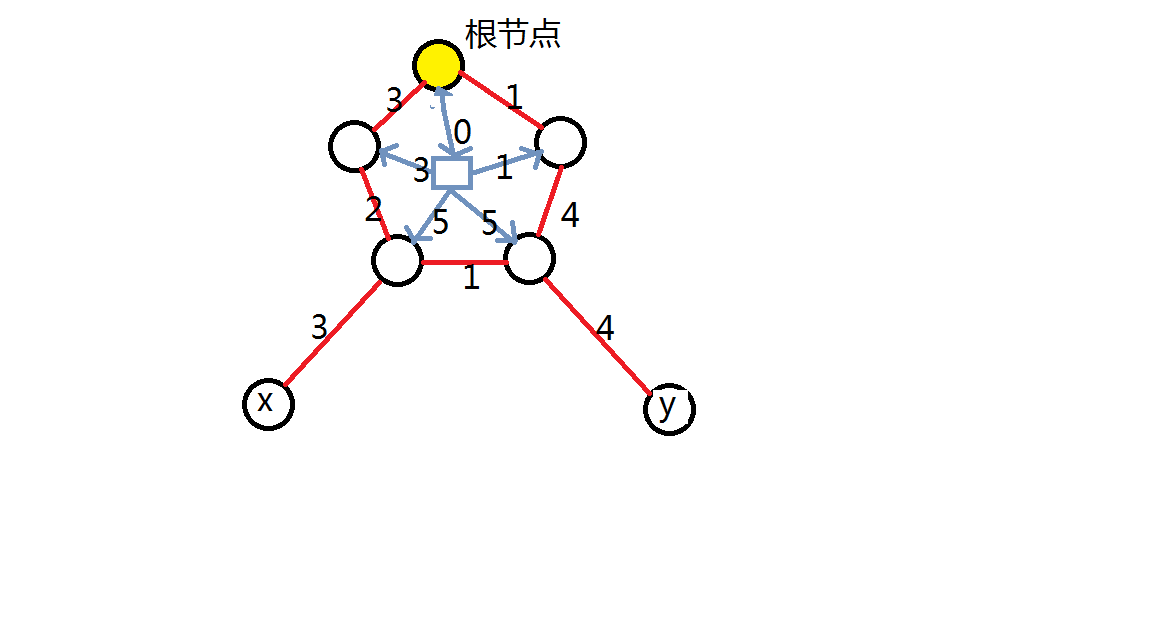
理论上是8，但lca会算出17
所以，若最近公共祖先是新建点，则要退一步求最短路
具体细节见代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=25005,t=15;
int head[N],ver[N<<1],edge[N<<1],ne[N<<1],fx[N<<1],tot;
int n,m,qu,ext;
int fa[N<<1],qw[N];
int la[N];
bool mark[N<<1];
int a[N<<1];
int d[N<<1],f[N][20],dist[N];
bool vis[N<<1];
map<PII,int> ma;
//建边 
void add(int x,int y,int z,int v)
{
    ver[++tot]=y,edge[tot]=z,fx[tot]=1,fx[tot]=v;
    ne[tot]=head[x],head[x]=tot;
}
//处理环 
void cl(int s,int e,int v)
{
    //新建点 
    ext++;
    //将环上所有点相互连接的边删去
    for(int i=s;i!=e;i=fa[i])
    {
        vis[qw[i]]=1;
        vis[qw[i]^1]=1;
        if(i==e) break;
    }
    vis[v]=1;
    vis[v^1]=1;
    //预处理 
    int cnt=1;
    a[cnt]=edge[v];
    for(int i=s;i!=e;i=fa[i])
    {
        cnt++;
        a[cnt]=a[cnt-1]+edge[qw[i]];
    }
    //环的长度 
    la[ext]=a[cnt];
    //并将环上所有点与新建点连接 
    for(int i=s,j=1;;i=fa[i],j++)
    {
        //入新建点,边权为0,1无意义 
        add(i,ext,0,1);
        //出新建点,边权为min(a[j],a[cnt]-a[j]),1/0表示方向,一样同向,不一样反向 
        if(a[j]<(a[cnt]-a[j])) add(ext,i,a[j],1);
        else add(ext,i,a[cnt]-a[j],0);
        //记录边 
        ma[{ext,i}]=tot;
        if(i==e) break;
    }
}
void dfs(int x,int p)
{
    //标记 
    mark[x]=1;
    for(int i=head[x];i;i=ne[i])
    {
        int y=ver[i],z=edge[i];
        //被删去的边,新的节点,走过来的边不行 
        if((vis[i])||(y>n)||(p==i)||((p^1)==i)) continue;
        //若仍找到标记的点,则找到环 
        if(mark[y])
        {
            //处理该环 
            cl(x,y,i);
            continue;
        }
        //记录y节点从那个节点来 
        fa[y]=x;
        //记录连接两点的边 
        qw[y]=i;
        //继续dfs 
        dfs(y,i);
    }
}
//讲解略 
void bfs()
{
    queue<int> q;
    q.push(1);
    d[1]=1;
    while(q.size())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=ne[i])
        {
            int y=ver[i],z=edge[i];
            if(vis[i]||d[y]) continue;
            d[y]=d[x]+1;
            dist[y]=dist[x]+z;
            f[y][0]=x;
            for(int i=1;i<=t;i++) f[y][i]=f[f[y][i-1]][i-1];
            q.push(y);
        }
    }
}
int lca(int x,int y)
{
    //基本操作 
    int ans=dist[x]+dist[y];
    if(d[x]>d[y]) swap(x,y);
    for(int i=t;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i];
    if(x==y) return ans-2*dist[x];
    for(int i=t;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    if(f[x][0]<=n) return ans-2*dist[f[x][0]];
    //最近公共祖先为新建点有所不同 
    else
    {
        //自己体会 
        int i,j;
        i=ma[{f[x][0],x}];
        j=ma[{f[y][0],y}];
        ans=ans-dist[x]-dist[y];
        if(fx[i]==fx[j]) return ans+min(abs(edge[i]-edge[j]),la[f[x][0]]-abs(edge[i]-edge[j]));
        else return ans+min(abs(edge[i]+edge[j]),la[f[x][0]]-abs(edge[i]+edge[j]));
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&qu);
    //ext表示新建点和原来点的个数总和 
    ext=n;
    //方便过会的xor的成对变换 
    tot++;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        //建边,1无意义 
        add(x,y,z,1);
        add(y,x,z,1);
    }
    //寻找环 
    dfs(1,0);
    //预处理 
    bfs();
    for(int i=1;i<=qu;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        //求最短路 
        printf("%d\n",lca(x,y));
    }
    return 0;
}