1. 解题思路

思路同01背包问题。区别在于01背包对于每种物品只有选或不选，这也即「01」的由来。多重背包则对于每种物品可以多次选择。

2. 解题代码（C++）

2.1 版本1 暴力做法 $O(n^3)$

本题数据加强后会TLE，主要理解思路即可。

• 状态f[i][j]定义（同「01背包问题」）：前 $i$ 个物品，背包容量 $j$ 下的最优解（最大价值）。
• 每一轮循环 i 都可以看作是对第 $i$ 件物品的决策——选择多少个（范围 $0$ ~ $\lfloor\frac{j}{v} \rfloor $）第 $i$ 件物品。
• 稍微不同的是多重背包允许多次选择一个物品，所以计算状态方程时需要枚举选择第 $i$ 个物品。

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 10000;
int v[MAXN];    // 体积 
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n;
    int m;  // 背包体积 
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++) 
        {
            int amount = j / v[i];  // j体积时物品最多能选的次数    
            for(int k = 0; k <= amount; k++) // 枚举选择第i个物品的个数
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);   // 状态转移方程
        }

    cout << f[n][m] << endl;
    return 0;
}

2.2 版本2 优化时间 $O(n^2)$

实际上，我们在计算状态方程时不必多一个循环去单独枚举选择第 $i$ 个物品个数。

状态转移方程推导如下：

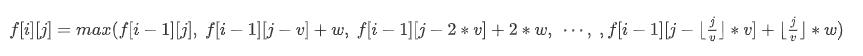
上述方程可以这样理解：我们计算的是前 $i$ 个物品 $j$ 体积的最优解$f[i][j]$ ，而前 $i-1$ 个物品的最优解 $f[i-1][j]$ 在上一轮循环中都已计算完毕，现在我们只需判断选择几个第 $i$ 种物品得到的价值最大。

我们改变一下变量，将 $j$ 变成 $j-v$，则有：

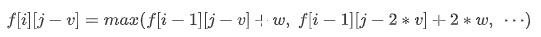
由以上两个式子就可以得到状态转移方程：

$f[i][j] = max(f[i-1][j],\ f[i][j-v])$

我们枚举体积 j 是从小到大的，那么我们在计算 f[i][j] 时，f[i][较大体积]总是由f[i][较小体积]更新而来。

代码如下：

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 10000;
int v[MAXN];    // 体积 
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n;
    int m;  // 背包体积 
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    f[0][0] = 0;
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++) 
        {
            f[i][j] = f[i - 1][j];  // 不选第i个物品
            if(j >= v[i])           // 可以选择第i个物品，状态方程见上面推导    
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

2.3 版本3 优化空间到一维

状态转移方程：f[j] = max(f[j], f[j - v[i]] + w[i])

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 10000;
int v[MAXN];    // 体积 
int w[MAXN];    // 价值 
int f[MAXN];    

int main() 
{
    int n;
    int m;  // 背包体积 
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)  
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }

    cout << f[m] << endl;
    return 0;
}

2.4 版本4 调整输入

我们注意到在处理数据时，我们是一个物品一个物品，一个一个单位体积进行枚举。

因此可以不必开两个数组记录体积和价值，而是边输入边处理。

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 10000;
int f[MAXN];    // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n;
    int m;  // 背包体积 
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;
        for(int j = v; j <= m; j++) {
            f[j] = max(f[j], f[j - v] + w);
        }
    }

    cout << f[m] << endl;
    return 0;
}