题目描述

有$ N $件物品和一个容量是$ V $的背包。每件物品最多只能使用一次。

第$ i$件物品的体积是$v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

分析

状态表示：二维
i: 只能从前i个物品中选
j：选出的所有物品的体积不能超过j

集合：给定i、j后所有物品的选法，后面将所有满足条件的选法记为集合(i, j)
属性：集合(i, j)中的每一种选法都对应一个价值，求的是集合(i, j)中所有选法所能够达的价值中最大的那一个，记为f[i][j]

----------------------------------------------------------------------------------------------------

状态计算：就是要想办法得到f[i][j]的表达式
f[i][j] = max(集合(i, j)内各种选法所产生的价值)
最直接的想法：想要求集合中的最大价值，就得知道集合中每一个元素的最大价值；
困难：直接这样做就成了暴力枚举 ==》能否将集合划分成不同的子集，这些子集的max值都已经求出？

划分集合：将集合内所有的选法按照是否包含第i个物品分成两类，记为：
S1(所有不含第i个物品的选法)；
S2(所有包含第i个物品的选法)；(前提条件，最大容积j能够保证物品i装入，否则S2就是空集)

f[i][j] = max(S1, S2) = max(max(S1), max(S2))
集合S1中所有的选法都没有物品i，因此所有的选法组成的集合就是(i-1, j)
max(S1) = max(集合(i-1, j)内所有的选法对应的价值) = f[i-1][j]
集合S2中所有的选法都有物品i，因此这些选法都可以看成是集合(i-1, j)中的所有选法+物品i产生的
max(S2) = max(集合(i-1, j-vi)内所有选法对应的价值) + wi = f[i-1][j-vi] + wi

综上，得到了状态转移方程
f[i][j] = max(f[i-1][j], f[i-1][j-vi] + wi) (j >= vi, 即S2非空)

代码实现(朴素版)

n, v = map(int, input().split())  # n件物品，容积最大为v

obj = []  # 所有物品
for i in range(n):
    obj.append(list(map(int, input().split())))  # obj[i][0]: 第i个物品的体积
                                                 # obj[i][1]: 第i个物品的价值

# f[i][j]：满足只使用前i件物品、最大体积不超过j的所有选法所能达到的最大价值
f = [[0] * (v + 1) for _ in range(n + 1)]

# 状态计算
for i in range(1, n + 1):
    for j in range(1, v + 1):
        f[i][j] = f[i - 1][j]       # 这种情况是一定存在的
        if (j >= obj[i-1][0]):      # 只有容积比第i个物品的体积大时，才有条件考虑第i个物品
            f[i][j] = max(f[i][j], f[i-1][j - obj[i-1][0]] + obj[i-1][1])

print(f[n][v])

空间优化思路

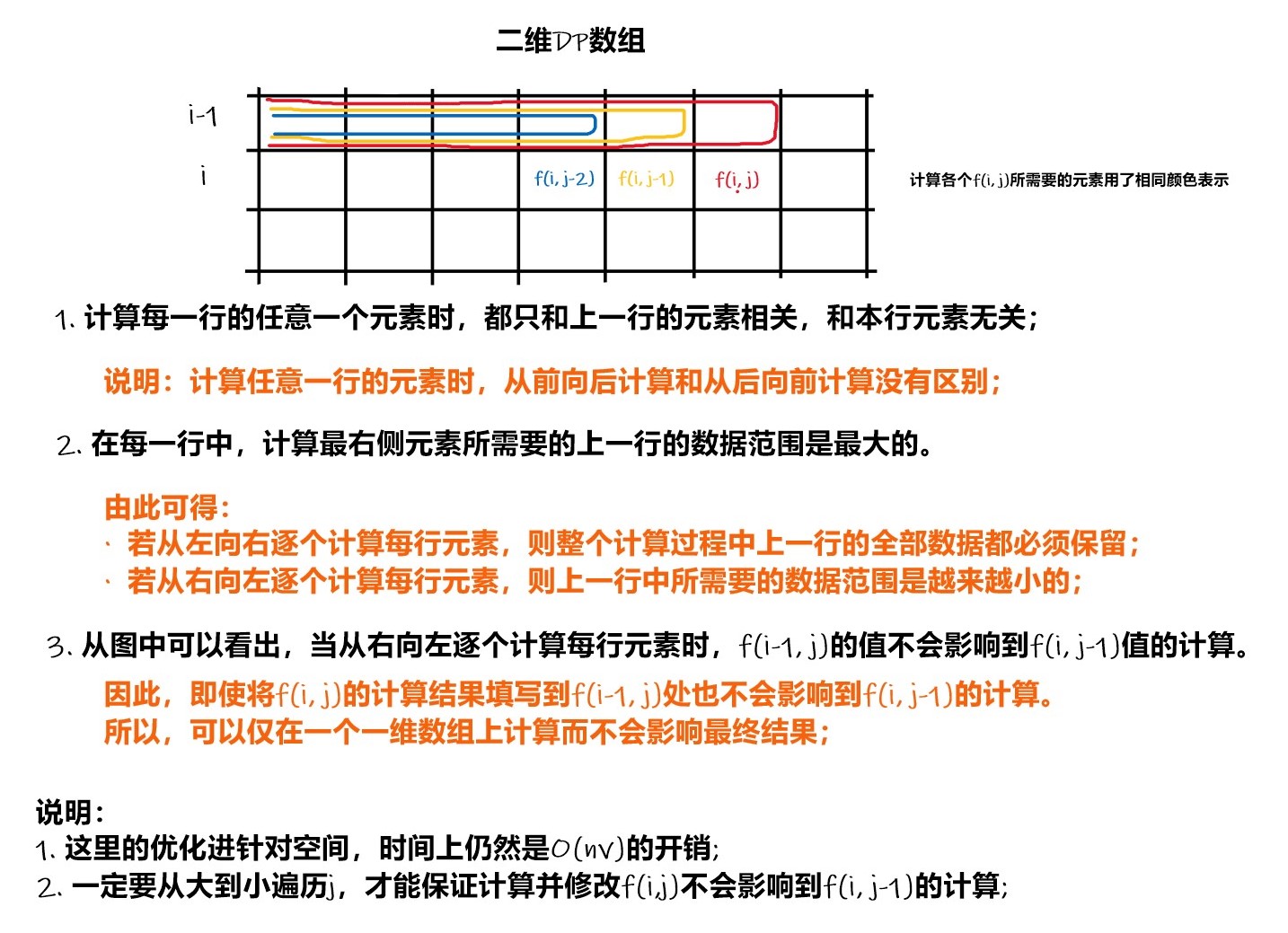
优化版本代码

说明: 优化后仍然是两种循环, 只是所需要的内存空间变小了;

n, v = map(int, input().split())  # n件物品，容积最大为v

obj = []  # 所有物品
for i in range(n):
    obj.append(list(map(int, input().split())))  # obj[i][0] 体积，obj[i][1] 价值

# dp数组
f = [0] * (v + 1)  # 直接初始化为0即可
for i in range(1, n + 1):
    for j in range(v, 0, -1):   # ！！！注意这里要从右向左遍历
        if j >= obj[i-1][0]:    # ！！！注意这里有等号
            f[j] = max(f[j], f[j-obj[i-1][0]] + obj[i-1][1])

print(f[v])