树状数组

引入问题

给出一个长度为$n$的数组，完成以下两种操作：
1. 将第$i$个数加上$k$
2. 输出区间$[i,j]$内每个数的和

朴素算法

1. 单点修改：$O(1)$
2. 区间查询：$O(n)$

使用树状数组

1. 单点修改：$O(logn)$
2. 区间查询：$O(logn)$

前置知识

$lowbit()$运算：非负整数$x$在二进制表示下最低位1及其后面的0构成的数值。

举例说明：
$lowbit(12) = lowbit([1100]_2) = [100]_2 = 4$

函数实现：

int lowbit(int x)
{
    return x & -x;
}

树状数组思想

树状数组的本质思想是使用树结构维护”前缀和”，从而把时间复杂度降为$O(logn)$。

对于一个序列，对其建立如下树形结构：

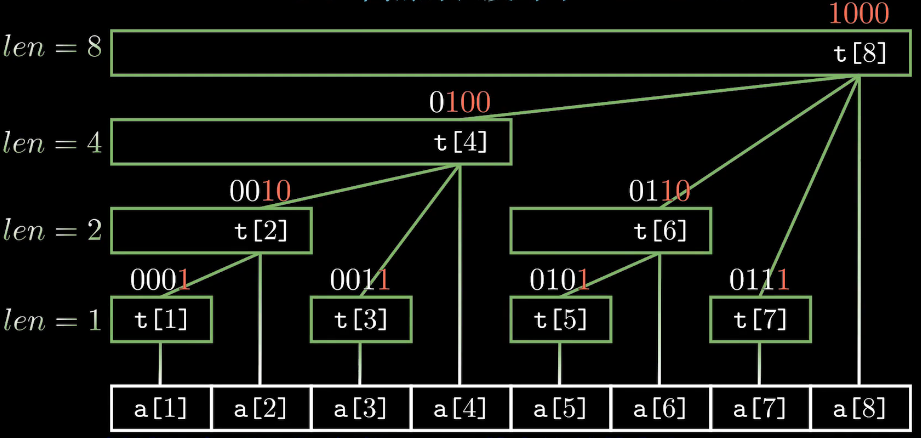
1. 每个结点t[x]保存以x为根的子树中叶结点值的和
2. 每个结点覆盖的长度为lowbit(x)
3. t[x]结点的父结点为t[x + lowbit(x)]
4. 树的深度为$log_2n + 1$

树状数组操作

• add(x, k)表示将序列中第x个数加上k。
  
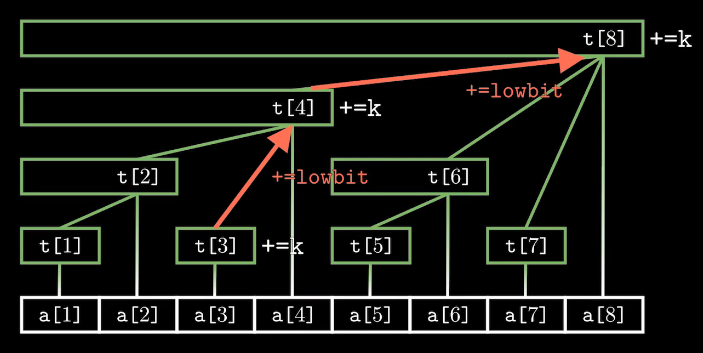
  以add(3, 5)为例：
  在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的t[x]值都加上k，这样保证计算区间和时的结果正确。时间复杂度为$O(logn)$。

void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += k;
}

• ask(x)表示将查询序列前x个数的和
  
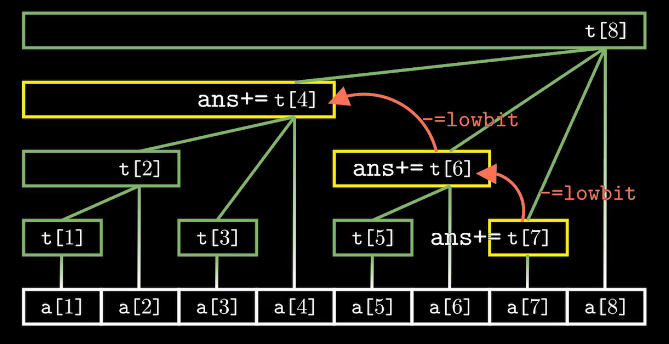
  以ask(7)为例：
  查询这个点的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值。向左上找到上一个结点，只需要将下标 x -= lowbit(x)，例如 7 - lowbit(7) = 6。

int ask(int x)
{
    int sum = 0;
    for(int i = x; i; i -= lowbit(i))
        sum += t[i];
    return sum;
}

以上关于树状数组的介绍来自于B站 。

本题题解

算法1

(暴力枚举) $O(n^2)$

一种朴素做法就是遍历所有点i， 分别统计i位置左边比a[i]小的数的个数m、右边比a[i]小的数的个数n，运用乘法原理：
1. 第一步从左边m个数中任选一个，有m种选法
2. 第二步从右边n个数中任选一个，有n种选法
那么在i位置组成图腾∧的方案数一共是 m * n。
累加每个点的方案数，即为所有组成图腾∧的方案总数。

时间复杂度$O(n^2)$。

C++ 代码

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 2000010;

typedef long long LL;

int a[N];
//ll[i]表示i的左边比第i个数小的数的个数
//rl[i]表示i的右边比第i个数小的数的个数
//lg[i]表示i的左边比第i个数大的数的个数
//rg[i]表示i的右边比第i个数大的数的个数
int ll[N], rl[N], lg[N], rg[N];

int main()
{
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j < i; j++)
        {
            //a[]保存的是1 ~ n的一个排列，不可能相等
            if(a[j] < a[i]) ll[i] ++;
            else lg[i] ++;
        }
    }

    for(int i = 1; i <= n; i++)
    {
        for(int j = n; j > i; j--)
        {
            if(a[j] < a[i]) rl[i] ++;
            else rg[i] ++;
        }
    }

    LL resV = 0, resA = 0;
    for(int i = 1; i <= n; i++)
    {
        resV += (LL)lg[i] * rg[i];
        resA += (LL)ll[i] * rl[i];
    }

    printf("%lld %lld\n", resV, resA);

    return 0;
}

算法2

(树状数组) $O(nlogn)$

1. 从左向右依次遍历每个数a[i]，使用树状数组统计在i位置之前所有比a[i]大的数的个数、以及比a[i]小的数的个数。
   统计完成后，将a[i]加入到树状数组。

2. 从右向左依次遍历每个数a[i]，使用树状数组统计在i位置之后所有比a[i]大的数的个数、以及比a[i]小的数的个数。
   统计完成后，将a[i]加入到树状数组。

时间复杂度 $O(nlogn)$

C++ 代码

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int N = 2000010;

typedef long long LL;

int n;
//t[i]表示树状数组i结点覆盖的范围和
int a[N], t[N];
//Lower[i]表示左边比第i个位置小的数的个数
//Greater[i]表示左边比第i个位置大的数的个数
int Lower[N], Greater[N];

//返回非负整数x在二进制表示下最低位1及其后面的0构成的数值
int lowbit(int x)
{
    return x & -x;
}

//将序列中第x个数加上k。
void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i)) t[i] += k;
}
//查询序列前x个数的和
int ask(int x)
{
    int sum = 0;
    for(int i = x; i; i -= lowbit(i)) sum += t[i];
    return sum;
}

int main()
{

    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);

    //从左向右，依次统计每个位置左边比第i个数y小的数的个数、以及大的数的个数
    for(int i = 1; i <= n; i++)
    {
        int y = a[i]; //第i个数

        //在前面已加入树状数组的所有数中统计在区间[1, y - 1]的数字的出现次数
        Lower[i] = ask(y - 1); 

        //在前面已加入树状数组的所有数中统计在区间[y + 1, n]的数字的出现次数
        Greater[i] = ask(n) - ask(y);

        //将y加入树状数组，即数字y出现1次
        add(y, 1);
    }

    //清空树状数组，从右往左统计每个位置右边比第i个数y小的数的个数、以及大的数的个数
    memset(t, 0, sizeof t);

    LL resA = 0, resV = 0;
    //从右往左统计
    for(int i = n; i >= 1; i--)
    {
        int y = a[i];
        resA += (LL)Lower[i] * ask(y - 1);
        resV += (LL)Greater[i] * (ask(n) - ask(y));

        //将y加入树状数组，即数字y出现1次
        add(y, 1);
    }

    printf("%lld %lld\n", resV, resA);

    return 0;
}