题目描述

Crane
Time Limit: 2000MS      Memory Limit: 65536K
Total Submissions: 11145        Accepted: 2935      Special Judge
Description

ACM has bought a new crane (crane -- jeřáb) . The crane consists of n segments of various lengths, connected by flexible joints. The end of the i-th segment is joined to the beginning of the i + 1-th one, for 1 ≤ i < n. The beginning of the first segment is fixed at point with coordinates (0, 0) and its end at point with coordinates (0, w), where w is the length of the first segment. All of the segments lie always in one plane, and the joints allow arbitrary rotation in that plane. After series of unpleasant accidents, it was decided that software that controls the crane must contain a piece of code that constantly checks the position of the end of crane, and stops the crane if a collision should happen. 

Your task is to write a part of this software that determines the position of the end of the n-th segment after each command. The state of the crane is determined by the angles between consecutive segments. Initially, all of the angles are straight, i.e., 180o. The operator issues commands that change the angle in exactly one joint. 
Input

The input consists of several instances, separated by single empty lines. 

The first line of each instance consists of two integers 1 ≤ n ≤10 000 and c 0 separated by a single space -- the number of segments of the crane and the number of commands. The second line consists of n integers l1,..., ln (1 li 100) separated by single spaces. The length of the i-th segment of the crane is li. The following c lines specify the commands of the operator. Each line describing the command consists of two integers s and a (1 ≤ s < n, 0 ≤ a ≤ 359) separated by a single space -- the order to change the angle between the s-th and the s + 1-th segment to a degrees (the angle is measured counterclockwise from the s-th to the s + 1-th segment).
Output

The output for each instance consists of c lines. The i-th of the lines consists of two rational numbers x and y separated by a single space -- the coordinates of the end of the n-th segment after the i-th command, rounded to two digits after the decimal point. 

The outputs for each two consecutive instances must be separated by a single empty line.
Sample Input

2 1
10 5
1 90

3 2
5 5 5
1 270
2 90
Sample Output

5.00 10.00

-10.00 5.00
-5.00 10.00
Source

CTU Open 2005

算法1

题解

本来以为这是一个简单的线段树模板 不料始终不太明白线段树如何记录转动角度后的各个线段端的XY值

学习了网络上的一些博客题解 感觉似是而非 谈到复数 角度 向量等，有点不太好理解

现在这里将自己的理解记录如下

如图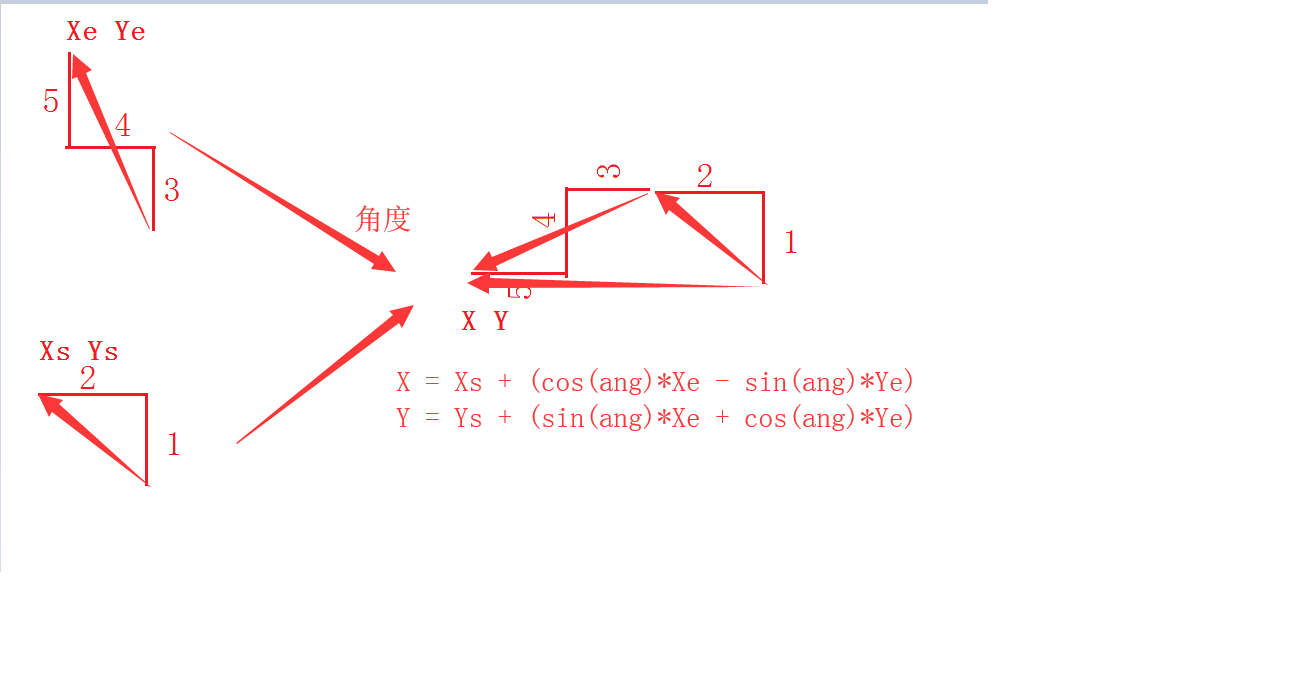
1 预备知识

使用线段树记录的内容如下 指示某段线段的组合 以第一条线段为垂直 最后的线段的端点的X Y值

途中1~2 线段 和3~5线段 就是线段树节点1~5的子节点 那么线段树节点1~5 就记录1~5结合后的X Y 值以及两个子节点结合的角度值

由于3~5线段的XY 是以自己的第一条线段为垂直起点为0 0 计算出来的X Y

那么在于1~2线段合并的时候 并不是简单的将两子节点的X Y相加即可得到1~5线段的XY 而是要加入旋转了相对角度 该角度由记录1~5线段的线段树节点记录

1~2线段部分的X Y值 旋转相对角度的公式推导如下

xNew = x * cosB - y * sinB

yNew = x * sinB + y * cosB

再来和 1~2线段的X Y相加即可得到1~5线段的X Y，并将该两子节点的相对角度记录在父节点中
预备知识讲完

2 解答步骤如下

一 建造线段树 build(1,1,n); 由于每条线段都是垂直连接 所以X 均为0 相对角度全部为0

void build(int k,int l,int r) {
    angT[k]=x[k]=0.0;
    if(r==l) y[k]=L[l];
    else {
        int lson=k*2, rson=k*2+1;
        int m=(l+r)/2;
        build(lson,l,m);
        build(rson,m+1,r);
        y[k]=y[lson]+y[rson];
    }
}

二 某段线段转动角度后

题意输入的角度是si和si+1逆时针角度而不是旋转的角度，而是需要转到的结果角度， 所以我们需要进行转换 。所以使用了pre数组记录每段线段与相邻线段的逆时针间隔角度，这样接收到题意输入角度a后

a-pre[s] 就是实际要转动的角度 而且需要更新pre[s] 以便下次计算

change(s,ang-pre[s],1,1,n);
pre[s]=ang; // 要求改变为a度 考虑之前已改变过
chang()代码就是批量更新需要转换的角度和X Y

只有旋转的起点线段在当前线段树节点的左子节点 我们才更新当前线段树节点的角度记录

如图

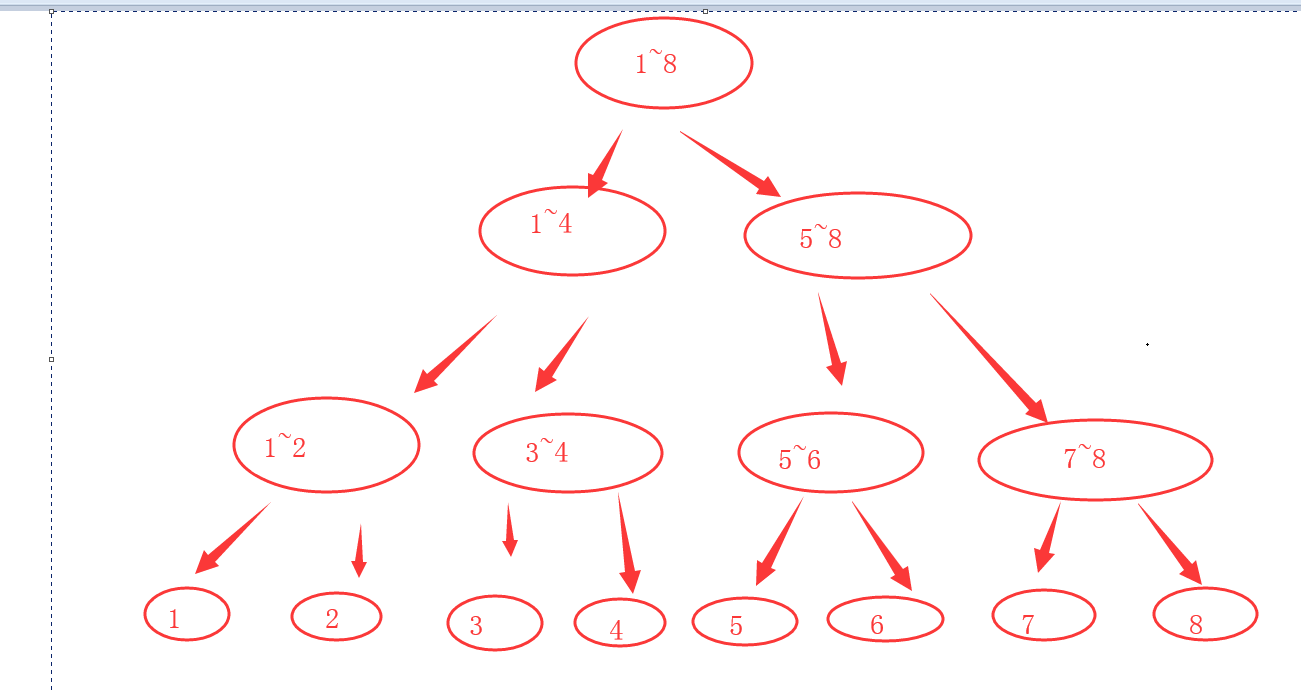
假设节点4 向3旋转90度

那么合并1 2的时候无更新

合并3 4的时候 3~4节点的角度要在原来记录上再旋转90

合并1~2 3~4为1~4的时候无需更新角度 因为 3~4 已经旋转 与1 ~2的相对角度 并没有变化

同样 5~8节点流程中无变化

但是合并1~4 5~8节点的时候 角度需要旋转90

整个流程下来 4 5~8 角度均旋转更新1次 符合题目的集合意义

最后返回1~8节点记录的X Y即可

代码如下

#include <iostream>
#include <vector>
#include <math.h>
#include <stdio.h>
using namespace std;
const double PI = acos(-1.0);
const int N = 10005;

int n, c, L[N];
double pre[N];

double angT[N << 2];
double x[N << 2], y[N << 2];

void build(int k, int l, int r) {
    angT[k] = x[k] = 0.0;
    if (r == l) y[k] = L[l];
    else {
        int lson = k * 2, rson = k * 2 + 1;
        int m = (l + r) / 2;
        build(lson, l, m);
        build(rson, m + 1, r);
        y[k] = y[lson] + y[rson];
    }
}


void change(int s, double ang, int k, int l, int r) {
    if (s < l || l == r) return; // 操作位置不在范围内 或 区间长度为1 不作处理
    else if (s <= r) {
        int lson = k * 2, rson = k * 2 + 1;
        int m = (l + r) / 2;
        change(s, ang, lson, l, m);
        change(s, ang, rson, m + 1, r); // 先处理左右子区间
        if (s <= m) angT[k] += ang; // 操作位置位于区间的左子区间内 可根据左右子区间的向量更新

        double sina = sin(angT[k]), cosa = cos(angT[k]);
        x[k] = x[lson] + (x[rson] * cosa - y[rson] * sina);
        y[k] = y[lson] + (x[rson] * sina + y[rson] * cosa);
    }
}


/*
Sample Input

2 1
10 5
1 90

3 2
5 5 5
1 270
2 90
Sample Output

5.00 10.00

-10.00 5.00
-5.00 10.00
*/

int main()
{
    while (~scanf("%d%d", &n, &c)) {
        for (int i = 1; i <= n; i++) {
            scanf("%d", &L[i]);
            pre[i] = PI;
        }
        build(1, 1, n);
        while (c--) {
            int s, a; scanf("%d%d", &s, &a);
            double ang = (double)a / 180.0*PI;
            change(s, ang - pre[s], 1, 1, n);
            pre[s] = ang;
            printf("%.2f %.2f\n", x[1], y[1]);
        }
        printf("\n");
    }

    return 0;
}