0-1背包问题是最基本的背包问题，多重背包问题的优化思路是基于二进制的思想转化为0-1背包问题，具体来说

就是将多重背包性质的物品拆分成0-1背包性质的多个物品。

举例来说，物品A的体积v = 1，价值w = 2，数量s = 3；可以将这个物品拆分成两个物品A1和A2，拆分系数为

{1, 2}，也就是说A1的体积是v，价值是w，A2的体积是2v，价值是2w，它们的数量都是1。

这样就把多重背包问题转化成0-1背包问题了，解释一下就是

{选择0个物品A，选择1个物品A，选择2个物品A，选择3个物品A}

和

{不选A1也不选A2，选A1不选A2，选A2不选A1，选择A1和A2}

这两个集合从选法上是等价的，而后者是我们在0-1背包问题中比较熟悉的。

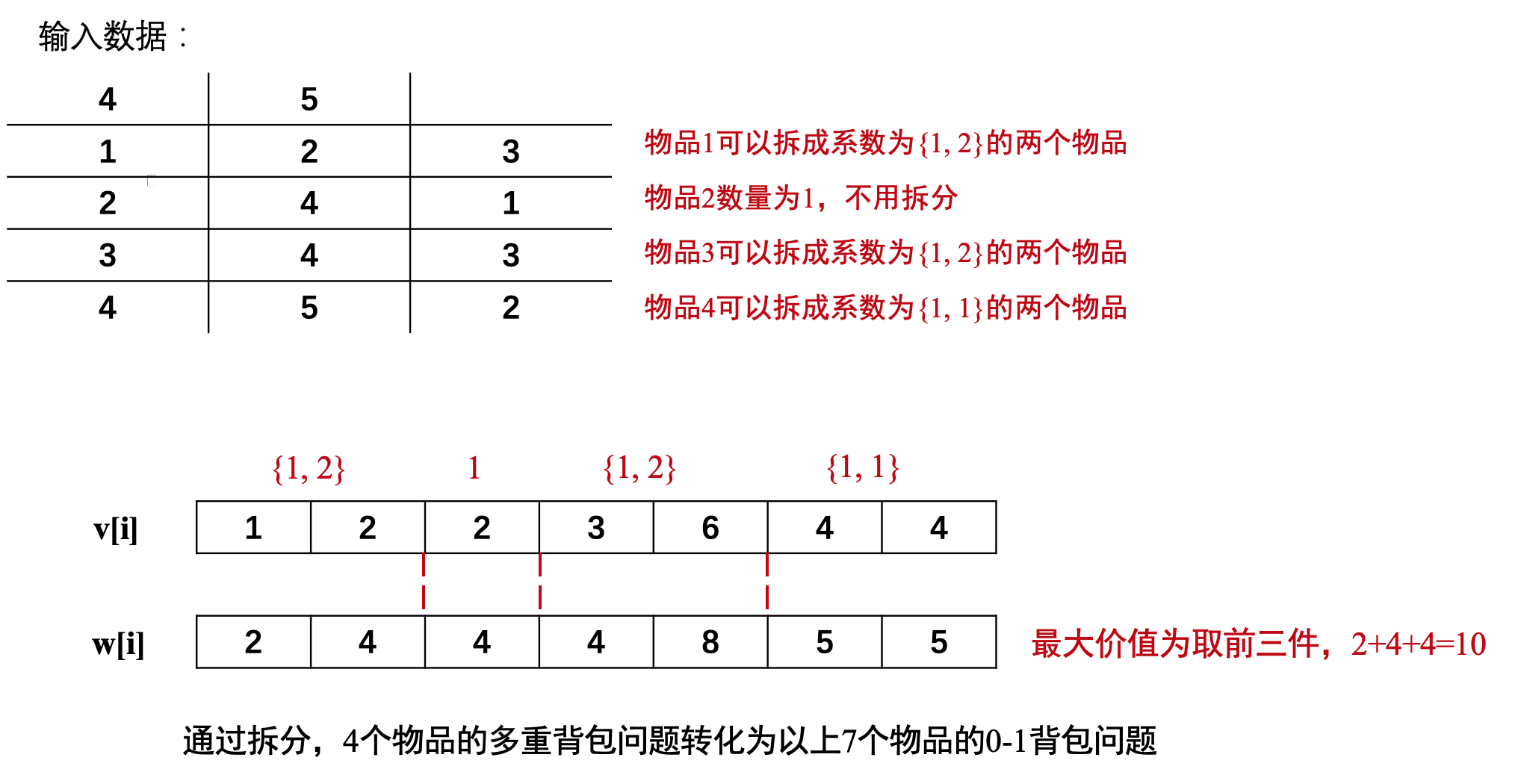
下面这张图就通过样例更为具体地解释了上面的思路：

#include <iostream>
using namespace std;
const int N = 12010, M = 2010;
int v[N], w[N], f[M];
int n, m;

int main() {
    scanf("%d%d", &n, &m);
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int a, b, s;
        scanf("%d%d%d", &a, &b, &s);
        int k = 1;
        while (k <= s) {
            ++cnt;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0) {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}