题目描述

你总共需要上 n 门课，课程编号依次为 0 到 n-1。

有的课会有直接的先修课程，比如如果想上课程 0，你必须先上课程 1，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries。

对于每个查询对 queries[i]，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

样例

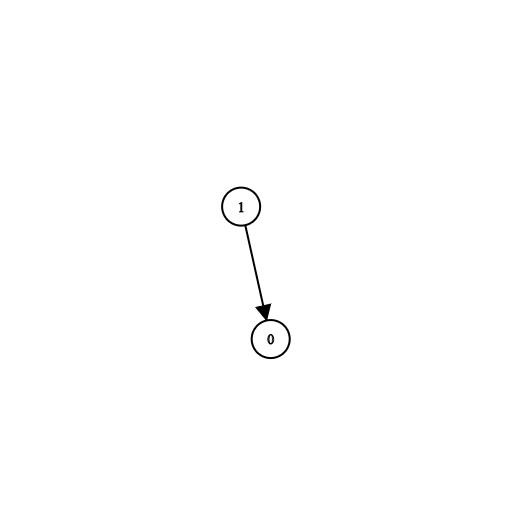
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

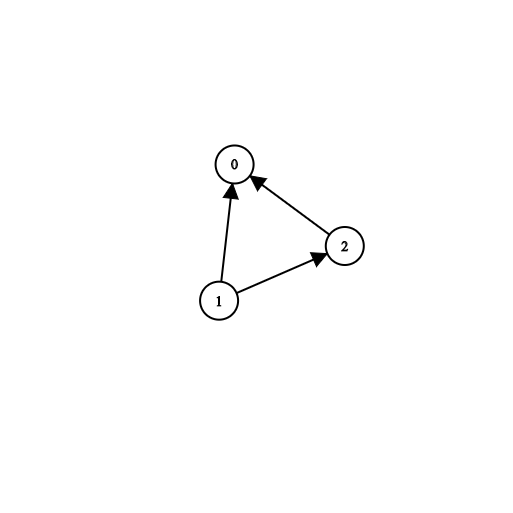
输入：
n = 3,
prerequisites = [[1,2],[1,0],[2,0]],
queries = [[1,0],[1,2]]

输出：[true,true]

输入：
n = 3,
prerequisites = [[1,0],[2,0]],
queries = [[0,1],[2,0]]

输出：[false,true]

输入：
n = 5,
prerequisites = [[0,1],[1,2],[2,3],[3,4]],
queries = [[0,4],[4,0],[1,3],[3,0]]

输出：[true,false,true,false]

限制

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• 先修课程图中没有环。
• 先修课程图中没有重复的边。
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

算法

(宽度优先遍历 / BFS) $O(n(n + m) + q)$

1. 建图之后，以每个点作为起点进行宽度优先遍历（或者深度优先遍历）。
2. 从 s 开始遍历到的点都以 s 作为先修课。
3. 预处理之后，对于每个询问，直接返回答案。

时间复杂度

• 每次遍历仅需要 $O(n + m)$ 的时间复杂度，故预处理的时间复杂度为 $O(n(n + m))$。
• 每个询问仅需要常数的时间，故总时间复杂度为 $O(n(n + m) + q)$。

空间复杂度

• 需要额外 $O(m)$ 的空间存储图，$O(n^2)$ 的空间存储预处理的答案，以及 $O(n)$ 的空间存储队列，$O(q)$ 的空间存储返回的答案。
• 故总空间复杂度为 $O(n^2 + q)$。

C++ 代码

class Solution {
public:
    vector<bool> checkIfPrerequisite(int n, 
                    vector<vector<int>>& prerequisites,
                    vector<vector<int>>& queries) {

        vector<vector<int>> graph(n);

        for (const auto &v : prerequisites)
            graph[v[0]].push_back(v[1]);

        vector<vector<bool>> tra(n, vector<bool>(n, false));
        for (int i = 0; i < n; i++) {
            queue<int> q;
            q.push(i);

            tra[i][i] = true;
            while (!q.empty()) {
                int u = q.front();
                q.pop();

                for (int v : graph[u])
                    if (!tra[i][v]) {
                        tra[i][v] = true;
                        q.push(v);
                    }
            }
        }

        vector<bool> ans(queries.size());
        for (int i = 0; i < queries.size(); i++)
            ans[i] = tra[queries[i][0]][queries[i][1]];

        return ans;
    }
};