题目描述

给定一个 rows x cols 的矩阵 grid 来表示一块樱桃地。grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

• 从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1)。
• 当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
• 当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
• 两个机器人在任意时刻都不能移动到 grid 外面。
• 两个机器人最后都要到达 grid 最底下一行。

样例

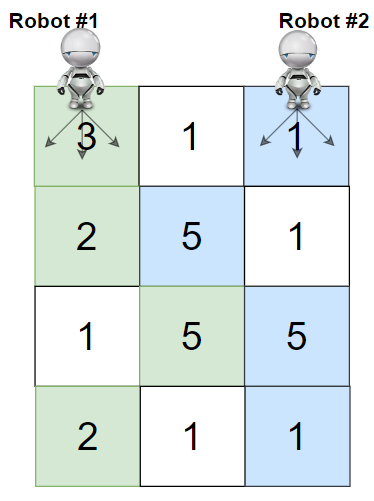
输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12。
樱桃总数为：12 + 12 = 24。

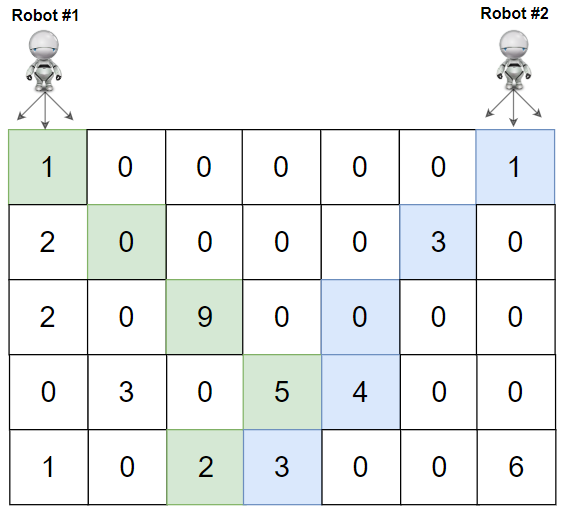
输入：
grid = [
    [1,0,0,0,0,0,1],
    [2,0,0,0,0,3,0],
    [2,0,9,0,0,0,0],
    [0,3,0,5,4,0,0],
    [1,0,2,3,0,0,6]
]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11。
樱桃总数为：17 + 11 = 28。

输入：grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出：22

输入：grid = [[1,1],[1,1]]
输出：4

限制

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

算法

(动态规划) $O(rc^2)$

1. 设状态 $f(i, j, k)$ 表示两个机器人分别位于第 $i$ 行的第 $j$ 和第 $k$ 列时的最大收益。
2. 初始时，由于宽度至少为 2，所以 $f(i, 0, c - 1) = grid[0][0] + grid[0][c - 1]$，其余为负无穷。
3. 转移时，如果 $j = k$，则 $f(i, j, k) = \max(f(i - 1, x, y) + grid[i][j])$，其中 $x$ 和 $y$ 表示在上一行时两个机器人可能的位置。如果 $j \neq k$，则同理转移 $f(i, j, k) = \max(f(i - 1, x, y) + grid[i][j] + grid[i][k])$。
4. 最终答案为 $\max(f(r - 1, j, k))$。

时间复杂度

• 状态数为 $O(rc^2)$，每次转移仅需要常数时间，故时间时间复杂度为 $O(rc^2)$。

空间复杂度

• 需要额外 $O(rc^2)$ 的空间存储状态。
• 可以通过滚动数组优化空间到 $O(c^2)$。

C++ 代码

class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        const int d[3] = {-1, 0, 1};
        const int N = 70;
        const int r = grid.size(), c = grid[0].size();

        vector<vector<vector<int>>> f(r,
            vector<vector<int>>(c, vector<int>(c, INT_MIN)));

        f[0][0][c - 1] = grid[0][0] + grid[0][c - 1];

        for (int i = 1; i < r; i++) {
            for (int j = 0; j < c; j++)
                for (int d1 = 0; d1 < 3; d1++) {
                    int x = j - d[d1];
                    if (x < 0 || x >= c) continue;

                    for (int k = 0; k < c; k++)
                        for (int d2 = 0; d2 < 3; d2++) {
                            int y = k - d[d2];
                            if (y < 0 || y >= c) continue;

                            if (j == k)
                                f[i][j][k] = max(f[i][j][k],
                                    f[i - 1][x][y] + grid[i][j]);
                            else
                                f[i][j][k] = max(f[i][j][k],
                                    f[i - 1][x][y] + grid[i][j] + grid[i][k]);
                        }
                }
        }

        int ans = 0;
        for (int j = 0; j < c; j++)
            for (int k = 0; k < c; k++)
                ans = max(ans, f[r - 1][j][k]);

        return ans;
    }
};