题目描述

你总共需要上n门课，课程编号依次为 0到 n-1。

有的课会有直接的先修课程，比如如果想上课程0 ，你必须先上课程 1 ，那么会以 [1,0]数对的形式给出先修课程数对。

给你课程总数 n和一个直接先修课程数对列表rerequisite 和一个查询对列表queries。

对于每个查询对 queries[i]，请判断queries[i][0]是否是queries[i][1]的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries每个查询对的判断结果。

注意：如果课程a是课程b的先修课程且课程b是课程c的先修课程，那么课程a也是课程c的先修课程。

提示：

$2 <= n <= 100$
$0 <= prerequisite.length <= (n * (n - 1) / 2)$
$0 <= prerequisite[i][0], prerequisite[i][1] < n$
$prerequisite[i][0] != prerequisite[i][1]$
先修课程图中没有环。
先修课程图中没有重复的边。
$1 <= queries.length <= 10^4$
$queries[i][0] != queries[i][1]$

样例

示例 1：

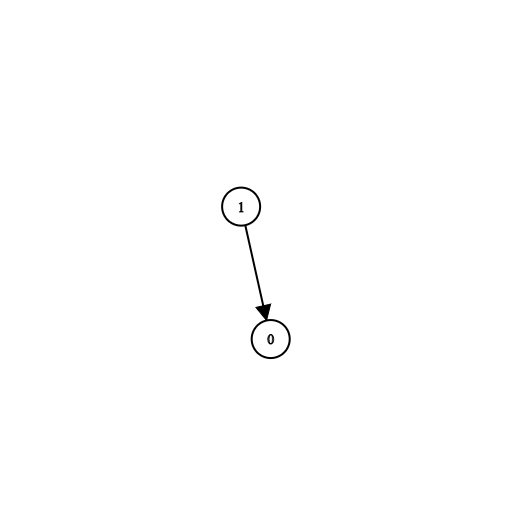
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

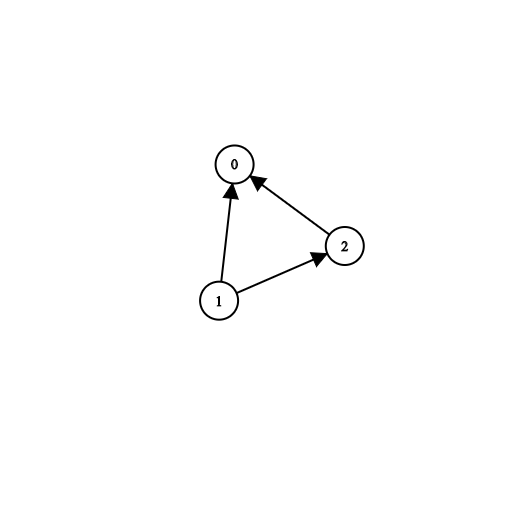
输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

示例 4：

输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]

示例 5：

输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]

算法1

(Floyd算法)

首先这道题可以转化为一个图的问题，而题目中的询问其实就是在问图中的两个点之间是否可达，因此我们可以使得有边的两个点之间的边权为0，其余边权均为正无穷，跑一遍Floyd算法，这样在处理询问的时候只有两点之间的距离为0时，才证明这两点是可达的，也就是前一个点是后一个点的先修课程。

时间复杂度

$O(n^3)$

java 代码

class Solution {
    int N = 110;
    int[][] g = new int[N][N];
    int max = 0x3f3f3f3f;

    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        for(int i=0; i<N; i++){
            Arrays.fill(g[i], max);
        }

        for(int[] cur : prerequisites){
            g[cur[0]][cur[1]] = 0;
        }

        for(int k=0; k<n; k++){
            for(int i=0; i<n; i++){
                for(int j=0; j<n; j++){
                    g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
                }
            }
        }

        List<Boolean> res = new ArrayList<Boolean>();

        for(int[] cur : queries){
            if(g[cur[0]][cur[1]] == 0) res.add(true);
            else res.add(false);
        }

        return res;
    }
}