题目描述

有 n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0。

样例

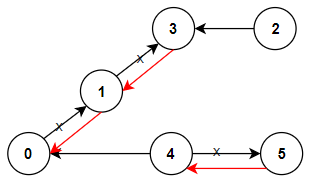
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0。

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0。

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

限制

• 2 <= n <= 5 * 10^4
• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

算法

(递归遍历) $O(n)$

1. 通过边集数组构造邻接表（且标记反边），从 0 号点开始递归遍历。
2. 如果发现当前点到儿子结点中的边是反向的，则累加答案。

时间复杂度

• 每个点仅遍历一次，故时间复杂度为 $O(n)$。

空间复杂度

• 递归需要额外 $O(h)$ 的系统栈空间，其中 $h$ 为树的最大高度。

C++ 代码

class Solution {
public:
    vector<vector<pair<int, bool>>> graph;
    int ans;

    void solve(int u, int fa) {
        int res = 0;
        for (const auto &p : graph[u])
            if (p.first != fa) {
                if (p.second) ans++;
                solve(p.first, u);
            }
    }

    int minReorder(int n, vector<vector<int>>& connections) {
        graph.resize(n);

        for (const auto &e : connections) {
            graph[e[0]].emplace_back(e[1], true);
            graph[e[1]].emplace_back(e[0], false);
        }

        ans = 0;
        solve(0, -1);

        return ans;
    }
};