题目描述

给定整数 n 和 k，找到 1 到 n 中字典序第 k 小的数字。

注意：1 ≤ k ≤ n ≤ 109。

样例

输入:
n: 13   k: 2

输出:
10

解释:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。

做过lc386的都知道可以dfs来进行十叉树的前序遍历来获得正确顺序。但是这题如果用dfs的话会超时，所以需要巧妙地剪枝

算法

(dfs剪枝)

假设答案在以节点cur为根的子树上(cur从1出发), 那么答案只有三个可能的落脚点 （1）cur本身 （2）与cur同层的下一个节点cur + 1，在以cur + 1为根节点的子树上 （3）在以cur的某个子节点为根的子树上 e.g. cur * 10, cur * 10 + 1, cur * 10 + 2, ..., cur * 10 + 9。

当答案为（1）时k为0。我们可以验证答案是否落在（2）上，通过计算以cur为根的子树大小，以cur, cur * 10, curr * 100, ..., curr * 10^k为左边界的枝节（inclusive）和以curr + 1， （curr + 1）* 10，..., (curr + 1) * 10 ^k为右边界(exclusive)中间的所有点。其中左边界上的所有点一定合法(<=n)。当右边界的点合法时 i.e. (curr + 1) * 10^k <= n + 1时，curr * 10 ^k~ (curr + 1) * 10^k之间的10^k个节点必然存在，需要从k中减去。但如果(curr + 1) * 10 ^k不合法，那么curr * 10 ^k~ n + 1之间的点也是存在的，需要从k中减去。

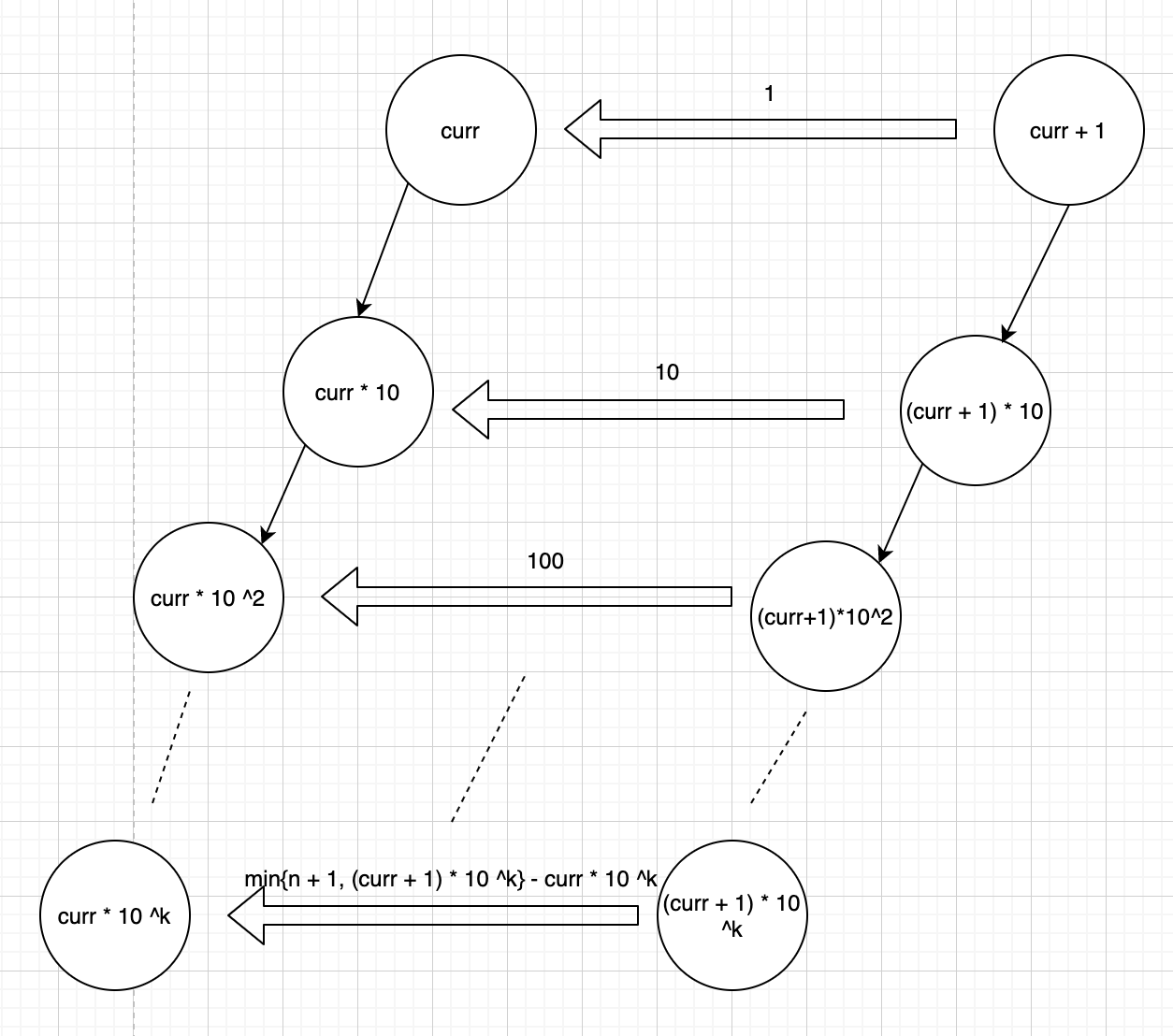
当我们把两边界之间的所有点都计算完后，我们得到子树大小step，如果step <= k则说明答案肯定在（3）上，否则在（2）上

时间复杂度

参考文献

C++ 代码

class Solution {
public:
    int findKthNumber(int n, int k) {
        // cur @ 当前节点， cur + 1 @ 同层下一个节点
        int cur = 1; --k;
        while(k > 0){
            // first @ 从cur往左下的左边界上的点, last @ 从cur + 1往左下的右边界上的点
            // step @ 计算以cur为根节点的子树大小
            long long first = cur, last = cur + 1, step = 0;
            // 计算子树大小
            while(first <= n){
                step += min((long long) n + 1, last) - first;
                first *= 10;
                last *= 10;
            }
            // case 1 @ 子树大小 <= k, 答案可能落在同层的下一个节点
            if(step <= k){
                k -= step;
                cur ++;
            }
            // case 2 @ 答案一定落在cur子树上，探索下一层
            else{
                k --;
                cur *= 10;
            }
        }
        return cur;
    }
};