题目描述

给出一个 N 个顶点 M 条边的无向无权图，顶点编号为 1 到 N。

问从顶点 1开始，到其他每个点的最短路有几条。
输入格式

第一行包含 2个正整数 N,M，为图的顶点数与边数。

接下来 M行，每行两个正整数 x,y，表示有一条顶点 x 连向顶点 y的边，请注意可能有自环与重边。

输出格式

输出 N行，每行一个非负整数，第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路，由于答案有可能会很大，你只需要输出对 100003取模后的结果即可。

如果无法到达顶点 ，则输出 0。

数据范围

1≤N≤105,
1≤M≤2×105

样例

输入样例：

5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5

输出样例：

1
1
1
2
4

题意：无向无权图，求从起点到每个点的最短路有多少条

到每个点的最短路的最后一条边可能有多条，同理，以最短路到达这些前驱边的边也有多条，只有求出最短路径较短的最短路条数才能求出路径较长的条数，很像是一个DP的问题，但是DP问题要要求依赖关系是一个拓扑序才可以。

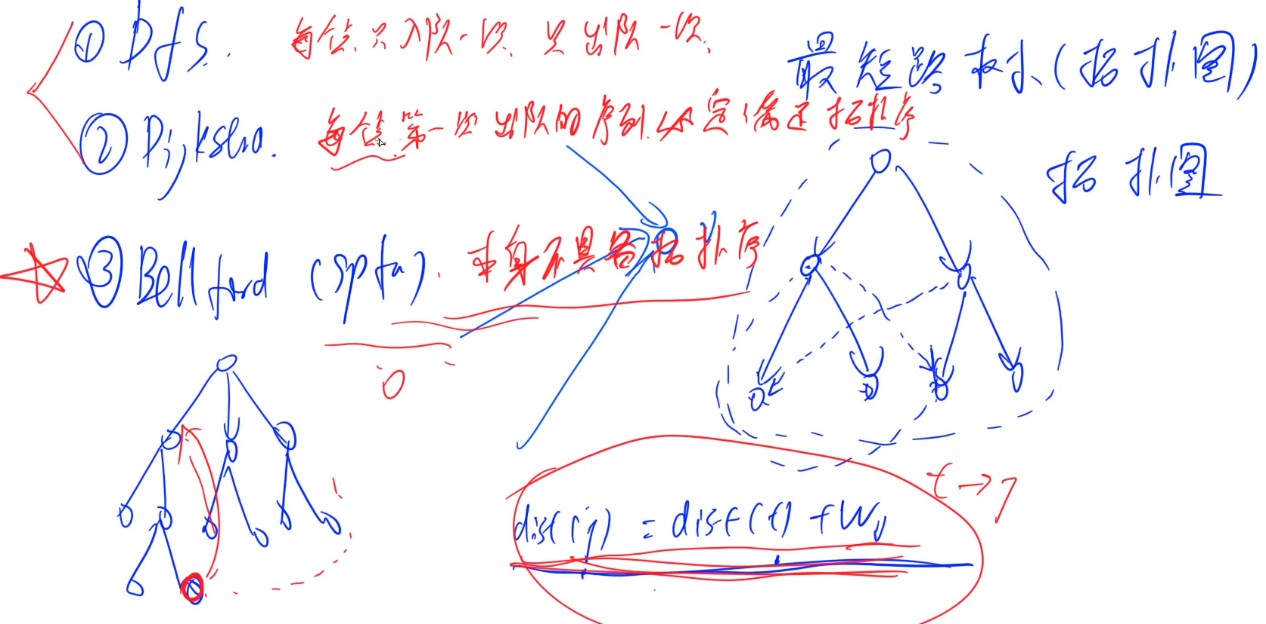
对于每一条最短路的边，有唯一的一个前驱和后继，将他们按照树的形式连接起来，那么就形成了最短路树，而树本来就是一个拓扑序的结构。但是有没有可能在建树的过程中构造出环，打破这个拓扑结构呢？在这个题目中，所有的边权=1，那么就是说要是A点从某条路径更新到达B点，而又存在另一条到达B点的最短路径在经过了A，B后再回到A，依旧是A的最短路径，就说明这个图中存在某个环，这个环的权值为0，显然是不存在的。所以可以认为这是一个拓扑序，那么就可以直接用BFS或者Dijstra来做，在更新路径的时候将点加入队列，如果遇到相等的路径就累加到点上即可。

（PS：但是利用SPFA是不可以做到的，因为SPFA在做最短路的时候，在图中是可能有负权边的，并且在出队和进队的时候都不可以保证是最小值，所以在再次到达某个点的时候最短路的长度可能并不会更新，那么也就无法得到准确的路径条数，就只能在得到最终的最短路径后再依据d[j]=d[t]+w[i]的关系来自行建立最短路树，再进行拓扑序的搜索得到结果）、

还是放一下上课的截图

C++ 代码

#include<iostream>
#include<cstring>
using namespace std;

const int N=1e5+10,M=400010,mod=100003;

int n,m;
int h[N],e[M],ne[M],idx;
int cnt[N],dist[N];
int q[N];

void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void BFS(){
    memset(dist,0x3f,sizeof dist);
    dist[1]=0,cnt[1]=1;
    int hh=0,tt=-1;
    q[++tt]=1;
    while(hh<=tt){
        int t=q[hh++];
        for(int i=h[t];~i;i=ne[i]){
            int j=e[i];
            if(dist[j]>dist[t]+1){
                dist[j]=dist[t]+1;
                cnt[j]=cnt[t];
                q[++tt]=j;
            }
            else if(dist[j]==dist[t]+1) cnt[j]=(cnt[j]+cnt[t])%mod;
        }
    }
}
int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }
    BFS();
    for(int i=1;i<=n;i++)   cout<<cnt[i]<<endl;
    return 0;
}