算法思路

​ 最直观的思路就是对两个数组进行归并，然后在归并数组中找到中位数即可。该算法时间复杂度为 O(m + n)

那么如何将算法优化到O(log(m + n))呢？

​ 由于两个数组大小确定，因此归并后的数组大小也是确定的，在确定长度的数组中找到中位数，寻找中位数的位置其实就是找到某K大数，即在数组中间位置的数。在归并过程中，我们线性扫描每个数组，最终找到中位数的位置。为了加快搜索速度，同时O(log(m + n))的时间复杂度提示我们可以采用二分的方法来对算法进行优化。

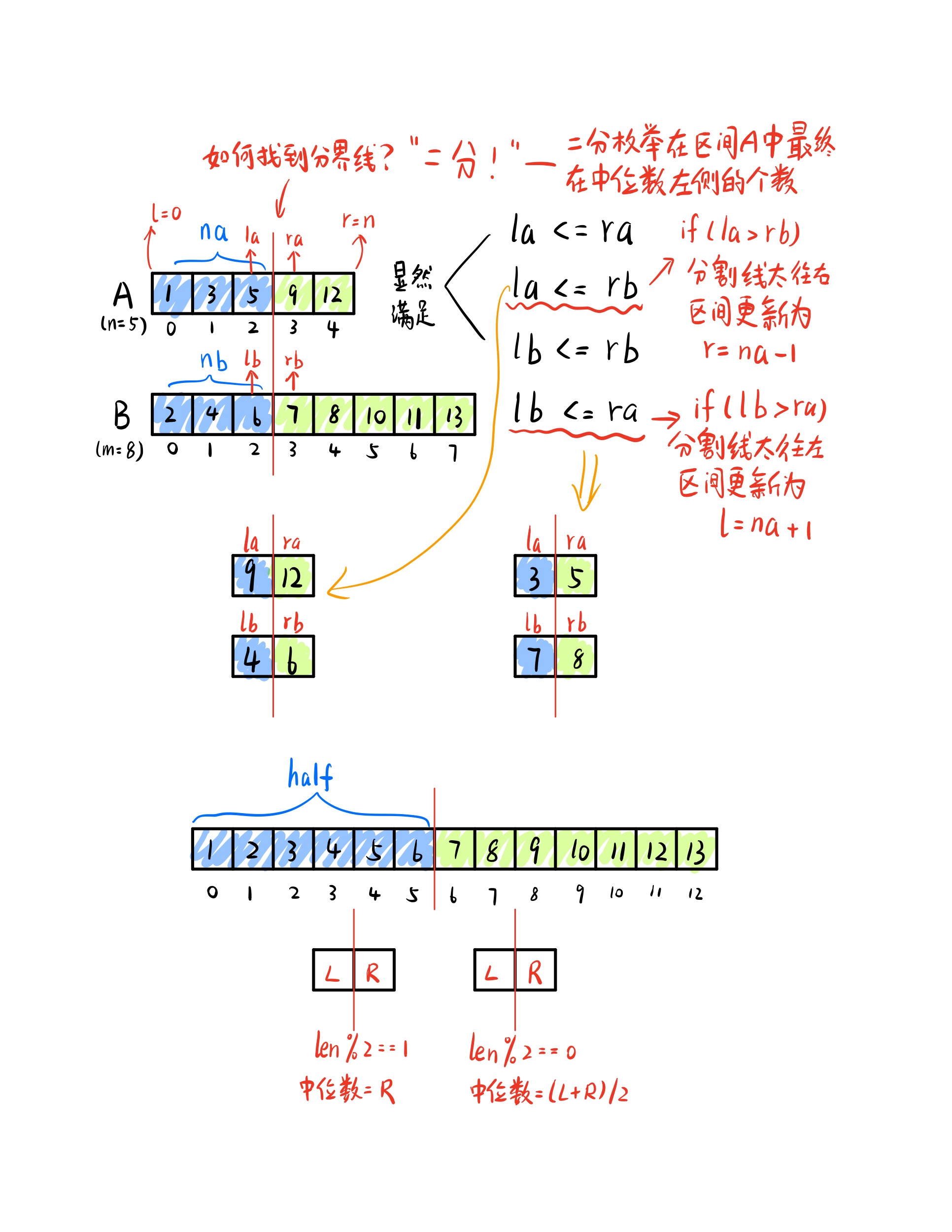
​ 在上图中可以看到，最终的数组可以分割为两个部分，左边部分是小于中位数的数，右边部分是大于中位数的数。同时，处于左边的数也一定来自于数组A和B的左边部分。因此我们可以枚举A数组中最终会出现在合并数组左边的数的个数。因为合并的数组大小是一定的，即小于中位数的个数也是一定的。所以说，如果A中所占的数越多，B中占的数也就越少。在图中直观表示为A中分割线左移对应B中分割线右移，反之相同。

​ 假设la, ra, lb, rb 分别表示为A数组和B数组分割线左右两侧的数，最终分割线的位置应该同时满足la <= ra, la <= rb, lb <= rb, lb <= ra,所以可以此为二分时的判断条件。最终找到分割线的位置，进而求出中位数。

​ 因为在求中位数时需要进行max, min比较，所以当分割线在边界时，将左右两侧边界值设定为INT_MIN和INT_MAX方便比较计算

C ++代码

class Solution {
public:
    double findMedianSortedArrays(vector<int>& A, vector<int>& B) {
       int n = A.size(), m = B.size();
       if (n > m) return findMedianSortedArrays(B, A);
       if (n == 0) return ((double)B[(m - 1) / 2] + (double)B[m / 2]) / 2;

       int len = n + m;
       int half = len / 2; //一半的个数

        int la = 0, ra = n; //A左边的数个数
        while (la <= ra)
        {
            int na = la + ra >> 1;

            int nb = half - na;
            double l1 = (na == 0) ? INT_MIN : A[na - 1];
            double r1 = (na == n) ? INT_MAX : A[na];
            double l2 = (nb == 0) ? INT_MIN : B[nb - 1];
            double r2 = (nb == m) ? INT_MAX : B[nb];

            if (l1 > r2) ra = na - 1;
            else if (l2 > r1) la = na + 1;
            else 
            {
                if (len % 2) return min(r1, r2);
                return (max(l1, l2) + min(r1, r2)) / 2;
            }
        }
        return -1;
    }
};

利用y总二分模板改进

利用y总的二分模板对上面的二分写法进行改进，所有思路与上面相同，我们需要二分的大小是A数组恰好在归并数组中中位数左边的个数.

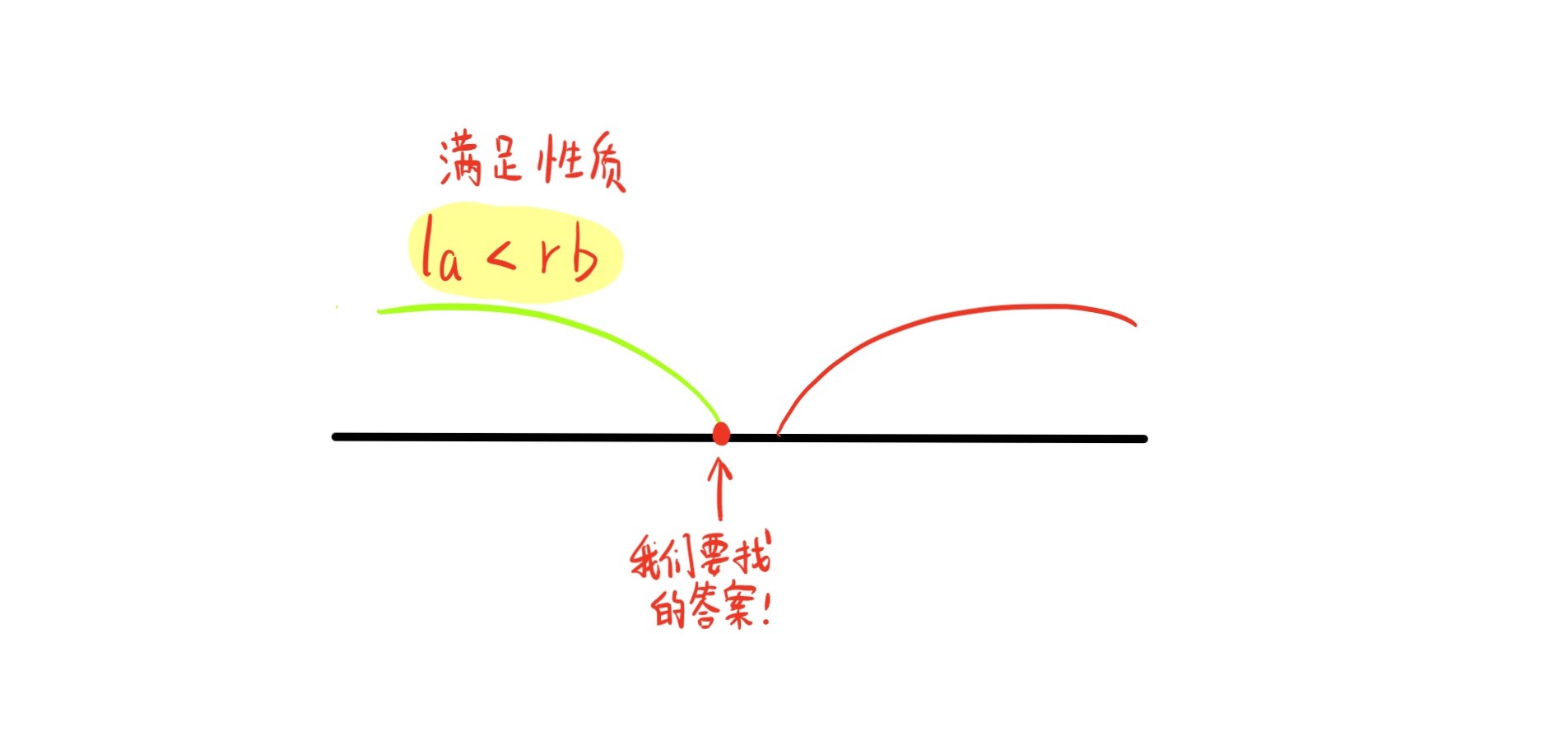
根据上面的分析思路可知，我们令A数组分界线左右两边值为la, ra, 根据y总二分模板的思路，我们需要找到一个性质，将区间一分为二，其中一边是满足该性质，一边不满足，且我们要找的答案就在某一区间的端点。

根据上图的分析，如果在数组A中的分界线在答案的左边，必然会满足la < rb, 如果分界线在答案的右边，即会出现la > lb,因此，我们要寻找的答案就在满足la < rb的区间的右端点。

因此采用模板

int b_search(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

C ++ 代码

class Solution {
public:
    int n,m;
    double findMedianSortedArrays(vector<int>& A, vector<int>& B) {
        if(A.size() > B.size()) return findMedianSortedArrays(B, A);
        n = A.size(), m = B.size();

        int l = 0, r = n;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (check(mid, A, B)) l = mid;
            else r = mid - 1;
        }

        int na = l, nb = (m + n) / 2 - na;
        double ans;

        double l1 = (na == 0) ? INT_MIN : A[na - 1];
        double r1 = (na == n) ? INT_MAX : A[na];
        double l2 = (nb == 0) ? INT_MIN : B[nb - 1];
        double r2 = (nb == m) ? INT_MAX : B[nb];

        if((n + m) & 1)  return min(r1, r2);
        return (max(l1, l2) + min(r1, r2)) / 2.0;

    }

    bool check(int i,vector<int>& A, vector<int>& B)
    {
        if(!i) return true;
        int j = (m + n) / 2 - i;
        if(A[i - 1] < B[j]) return true;
        return false;
    }
};