题目描述

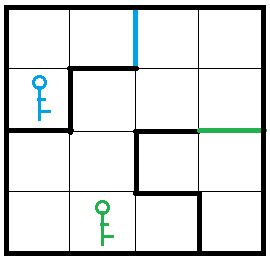
输入样例

4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0 
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2 
4 2 1

输出样例

14

算法

(拆点+BFS) $O(nm)$

1. 将迷宫中的二维坐标压缩成一维数组方便枚举，即$n$行$m$列的迷宫中点$(x, y)$的下标为$t = (x - 1) * n + y$
2. 设$dist[t][state]$表示所有从起点走到$t$这个格子，且当前已经拥有的钥匙是$state$的所有路线的集合中的最短距离
3. 用一个10位的二进制数$state$存储每一类🔑的存放情况
4. 初始时，对于没有🔑的单元，只有一种状态$dist[t][0]$；对于包含🔑的单元，有两种状态$dist[t][0]$和$dist[t][state]$（因为只要有钥匙一定是全部带着，否则有可能走回头路）
5. 状态转移的方式分以下2种情况：
   • 拿起所有钥匙（花费时间0）：$dist[t][state] = min(dist[t][state], dist[t][0])$
   • 向四周移动，只有以下2种情况能走（花费时间1）：$dist[t1][state] = min(dist[t1][state], dist[t2][state] + 1)$
     （1）没有门和墙
     （2）有门，且有匹配的钥匙
6. 状态转移过程中花费时间只有0或者1，因此考虑使用双端队列BFS

时间复杂度

整个过程分为建图和双端队列广搜，每个单元至多只会入队和出队一次，因此时间复杂度是$O(nm)$

C++ 代码

#include <iostream>
#include <cstring>
#include <deque>
#include <set>
using namespace std;

#define x first
#define y second

typedef pair<int, int> PII;
const int N = 11, M = N * N, E = 400, P = 1 << N;

int n, m, p, k;
int h[M], e[E], w[E], ne[E], idx;
int g[N][N], keys[M], dist[M][P];
bool st[M][P];
set<PII> edges;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void build() {
    int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            for (int u = 0; u < 4; u ++ ) {
                int x = i + dx[u], y = j + dy[u];
                if (x <= 0 || y <= 0 || x > n || y > m) continue;
                int a = g[i][j], b = g[x][y];
                if (!edges.count({a, b})) add(a, b, 0);
            }
}

int bfs() {
    memset(dist, 0x3f, sizeof dist);
    dist[1][0] = 0;

    deque<PII> q;
    q.push_back({1, 0});

    while (q.size()) {
        PII t = q.front(); q.pop_front();

        if (st[t.x][t.y]) continue;
        st[t.x][t.y] = true;

        if (t.x == n * m) return dist[t.x][t.y];

        if (keys[t.x]) {
            int state = t.y | keys[t.x];
            if (dist[t.x][state] > dist[t.x][t.y]) {
                dist[t.x][state] = dist[t.x][t.y];
                q.push_front({t.x, state});
            }
        }

        for (int i = h[t.x]; ~i; i = ne[i]) {
            int j = e[i];
            if (w[i] && !(t.y >> w[i] - 1 & 1)) continue;
            if (dist[j][t.y] > dist[t.x][t.y] + 1) {
                dist[j][t.y] = dist[t.x][t.y] + 1;
                q.push_back({j, t.y});
            }
        }
    }

    return -1;
}

int main() {
    cin >> n >> m >> p >> k;

    int cnt = 1;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            g[i][j] = cnt ++ ;

    memset(h, -1, sizeof h);

    for (int i = 0; i < k; i ++ ) {
        int x1, x2, y1, y2, c; cin >> x1 >> y1 >> x2 >> y2 >> c;
        int a = g[x1][y1], b = g[x2][y2];
        if (c) add(a, b, c), add(b, a, c);
        edges.insert({a, b}), edges.insert({b, a});
    }

    build();

    cin >> p;
    for (int i = 0; i < p; i ++ ) {
        int x, y, c; cin >> x >> y >> c;
        keys[g[x][y]] |= 1 << c - 1;
    }

    cout << bfs();

    return 0;
}