题目描述
 blablabla
blablabla
算法1
解法
依次遍历一次翻转K(1~N)头牛的办法 最后得出转数最小的答案 复杂度是 NNN
但是在模拟一次翻转K头牛的时候 我们可以优化模拟翻转的过程 优化效率
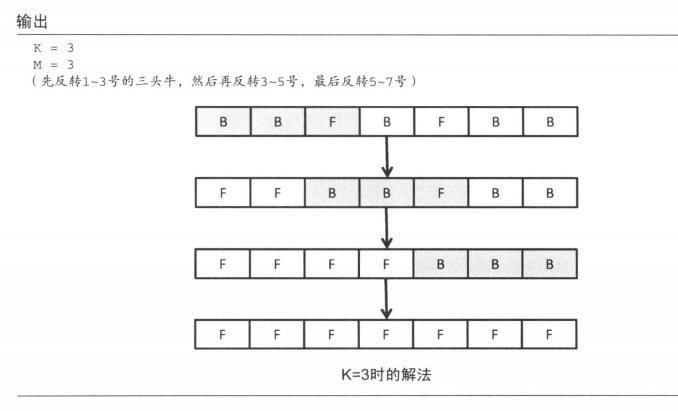
如图 当K = 3 每次翻转3头牛的时候
第0头牛 朝后 之前影响到第0头牛的点击数为0 所以我们需要点击1次 将牛朝前
第1头牛 朝后 之前影响第1头牛的点击数为1 所以牛已经朝前不必点击
第2头牛 朝前 之前影响第2头牛的点击数为1 所以需要点击1次 将牛朝前
第3头牛 朝后 之前影响第3头牛的点击数为1 牛已经朝前(之前其实点击了两次 但是第0头牛的点击只影响0 1 2 这3头牛)
第4头牛 朝前 之前影响第4头牛的点击数为1 牛朝后,需要点击1次
第5头牛 朝后 之前影响第5头牛的点击数为1 牛朝前
第6头牛 朝后 之前影响第6头牛的点击数为1 牛朝前
点击牛的个数 0 2 4 ,共3次点击.
如果我们在遍历到第i头牛的时候 已经记录之前能影响到i头牛的点击数 就不必每次去模拟一次点击后牛的朝向
那么 整体复杂度就从 nnn 降低到n*n
代码如下:
C++ 代码
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int MAX_N = 5e3 + 10;
int f[MAX_N]; int N;
int d[MAX_N];
int getans(int k)
{
memset(f, 0, sizeof(f));
int sum = 0; int res = 0;
for (int i = 0; i + k <= N; i++) {
//第i头牛 和之前能影响到它的点击数和 如果余1 则说明该牛朝后 需要点击
if ((d[i] + sum) % 2 == 1) {
f[i] = 1; res++;
}
sum += f[i];
//i向后推移 则减去影响不到i头牛的点击数字
if (i - k + 1 >= 0) sum -= f[i - k + 1];
}
//最后k-1头牛是不必点击的 只需要查看他们被影响的点击和 判断是否朝前
for (int i = N - k + 1; i < N; i++) {
if ((d[i] + sum) % 2 == 1)
return -1;
if (i - k + 1 >= 0) sum -= f[i - k + 1];
}
return res;
}
int main()
{
while (cin >> N) {
for (int i = 0; i < N; i++) {
char c; cin >> c;
if (c == 'F') d[i] = 0;
else d[i] = 1;
}
int K = 1; int M = N;
for (int k = 1; k <= N; k++) {
int m = getans(k);
if (m >= 0 && M > m) {
M = m; K = k;
}
}
cout << K << " " << M << endl;
}
return 0;
}

