题目描述

你总共需要上 n 门课，课程编号依次为 0 到 n-1 。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。

对于每个查询对 queries[i] ，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

样例

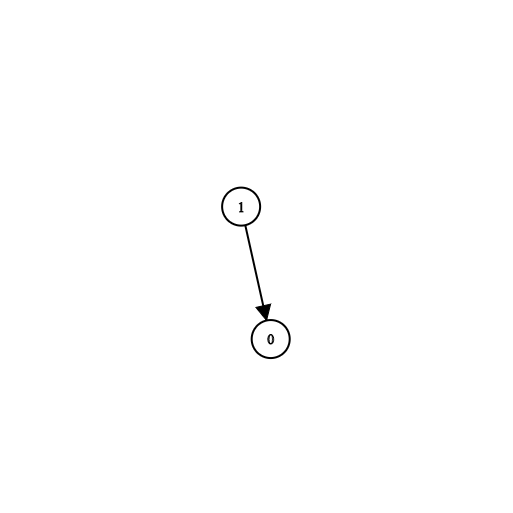
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

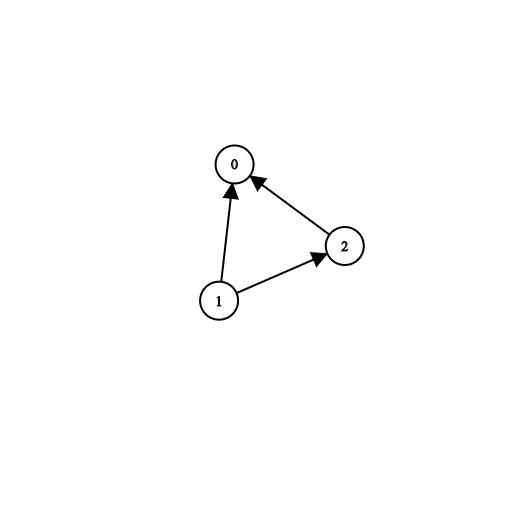
输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]

输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]

提示：

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• 先修课程图中没有环。
• 先修课程图中没有重复的边。
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

算法分析

floyd解决传递闭包问题，核心思想:i --> k且k --> j，则i -- > j

• 1、对课与课之间关系的二维数组跑一遍floyd，得到每个课与其他课的先后顺序
• 2、枚举queries数组，判断 a = queries[i][0] 是否是 b = queries[i][1] 的先修课程，若dist[a][b] == 1则表示是，否则表示不是

时间复杂度 $O(n^3)$

Java 代码

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        List<Boolean> ans = new ArrayList<Boolean>();
        int[][] dist = new int[110][110];
        for(int i = 0;i < prerequisites.length;i ++)
        {
            int x = prerequisites[i][0];
            int y = prerequisites[i][1];
            dist[x][y] = 1;
        }
        for(int k = 0;k < n;k ++)
            for(int i = 0;i < n;i ++)
                for(int j = 0;j < n;j ++)
                    if(dist[i][k] == 1 && dist[k][j] == 1)
                        dist[i][j] = 1;

        for(int i = 0;i < queries.length;i ++)
        {
            int x = queries[i][0];
            int y = queries[i][1];
            ans.add(dist[x][y] == 1);
        }
        return ans;
    }
}