中序遍历

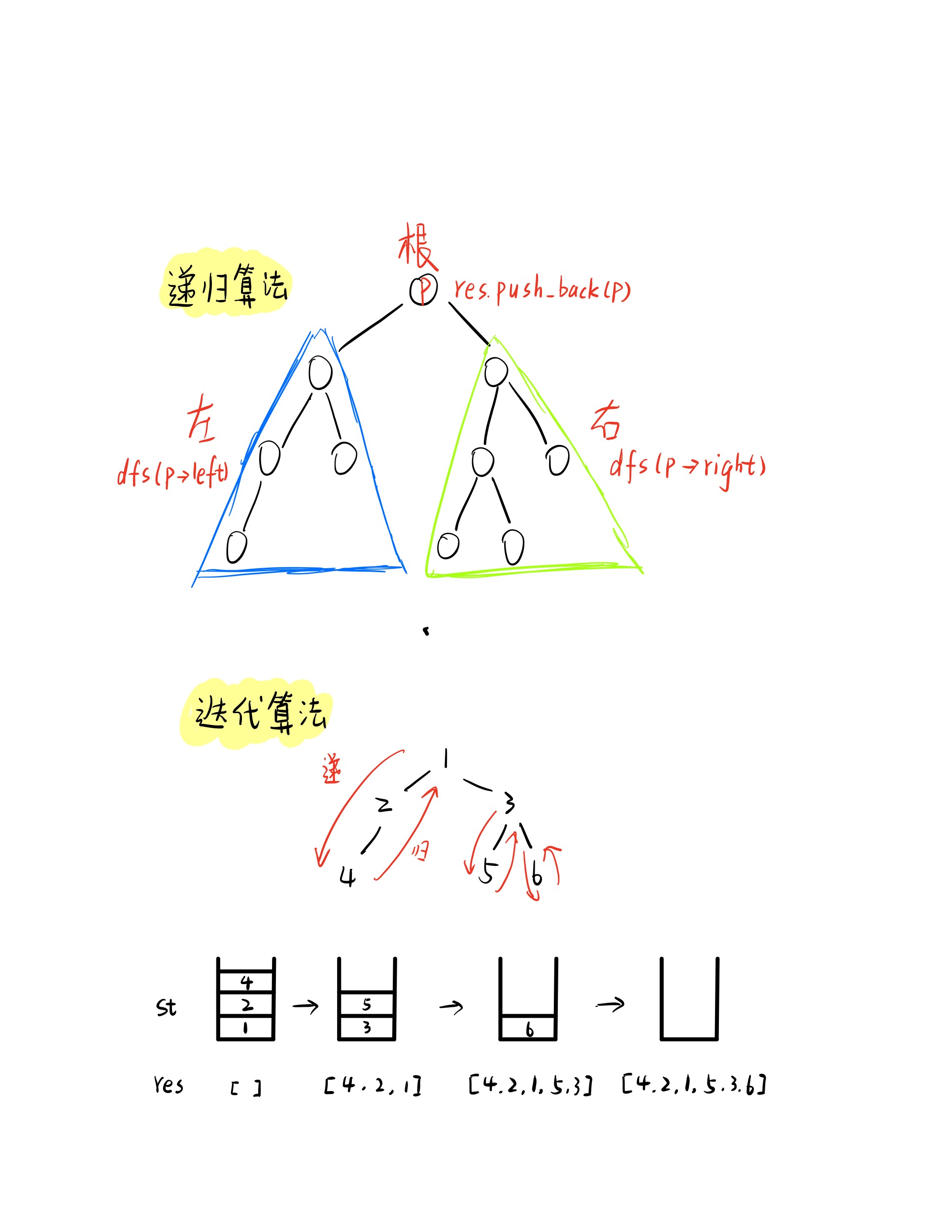
中序遍历过程的顺序是 左 -> 根 -> 右

递归算法

递归算法比较简单，就根据中序遍历的过程，先遍历左子树，再遍历当前根，然后遍历右子树。递归函数的中止条件是当前结点为空，同时当遍历当前结点时，将该点加入遍历数组即可。

调用递归函数时可以看作它已经帮你完成了你所想要完成的所有事，它已经将答案封装好交到了你的手上。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    vector<int> inorderTraversal(TreeNode* root) {
        dfs(root);
        return res;
    }

    void dfs(TreeNode* p)
    {
        if (!p) return;
        dfs(p -> left);
        res.push_back(p -> val);
        dfs(p -> right);
    }
};

迭代算法

递归函数实现的过程其实就是系统帮我们调用栈的过程，所以如果换为迭代算法来写，我们只需要自己模拟实现一个栈。

递归的实现也可以反映成一棵树，就是所谓的递归树，当我们调用递归函数的时候，其实有两个过程，一个是向下的递的过程，然后再是向上的归的过程。递归函数很好地封装了这一点，然而当我们用迭代算法时，需要自己去模拟递和归的过程。

遍历是，我们需要将所有左子树链上的所有点放入栈中，该过程即为递,然后取出栈顶，加入遍历数组，之后再放入右子树，同时注意这里的右子树指的是整个右子树的左子树链。直到遍历完所有结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;

        auto p = root;

        while (p || !st.empty())
        {
            while (p)
            {
                st.push(p);
                p = p -> left;
            }

            p = st.top();
            st.pop();
            res.push_back(p -> val);
            p = p -> right;
        }

        return res;
    }
};