题目描述

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

样例

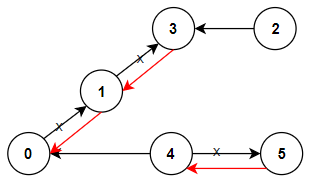
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示：

• 2 <= n <= 5 * 10^4
• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

算法分析

图论

题目：给定n个点，n - 1条有向边，因此两个之间只有一条有向边，为了令所有点均能达到0号点，因此需要将某些有向边a -> b，变成b -> a，问需要边多少条

• 1、建图，建图过程中，将两个点之间建双向边，若a -> b，需要通过edge[]数组记录下来，表示该边是题目给定的
• 2、从 0 结点开始深度遍历，枚举到u点时，u点是通过i边指向j点，若i边在edge[]数组中存在，则表示题目中u点到j点存在有向边，需要对该边调整过来，使得j -> u（因为是从0点反着走）

时间复杂度 $O(n)$

Java 代码

class Solution {
    static int N = 50010,M = 2 * N;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int idx = 0;
    static int ans ;
    static boolean[] edge = new boolean[M];
    static void add(int a,int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void dfs(int u,int father)
    {
        for(int i = h[u];i != -1;i = ne[i])
        {
            int j = e[i];
            if(j == father) continue;
            if(edge[i]) ans ++;
            dfs(j,u);
        }
    }
    public int minReorder(int n, int[][] connections) {
        Arrays.fill(h,-1);
        idx = 0;
        for(int i = 0;i < n - 1;i ++)
        {
            int a = connections[i][0];
            int b = connections[i][1];
            edge[idx] = true;
            add(a,b);
            add(b,a);
        }
        ans = 0;
        dfs(0,-1);

        return ans;
    }
}