题目描述

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中 horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离，类似地， verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7 取余后返回。

示例 1：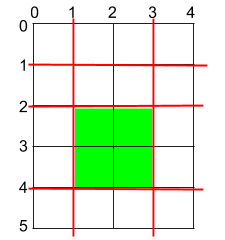
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

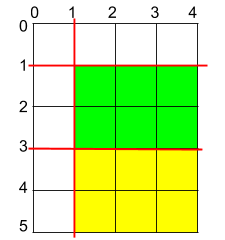
输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

算法1

主要是求出 横向 纵向切刀的距离最大值
而且向数组总加入开头的0坐标 和最后的长度坐标 有利于减少代码量

class Solution {
public:
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        horizontalCuts.push_back(0);horizontalCuts.push_back(h)  ;    
        verticalCuts.push_back(0);verticalCuts.push_back(w);

        sort(horizontalCuts.begin(),horizontalCuts.end());
        sort(verticalCuts.begin(),verticalCuts.end());

        int  maxh = -999;
        int  maxw = -999;
        for(int i=horizontalCuts.size()-1;i >0 ;i--){
            maxh = max(maxh,horizontalCuts[i]-horizontalCuts[i-1]);
        }

        for(int i =verticalCuts.size()-1;i>0;i-- ){
            maxw = max(maxw,verticalCuts[i]-verticalCuts[i-1]);
        }

        return  (long long )maxw*maxh%(1000000007);
    }
};