题目描述

你总共需要上 n门课，课程编号依次为 0到 n-1。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以[1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries。

对于每个查询对 queries[i] ，请判断queries[i][0]是否是queries[i][1]的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程

样例

样例1

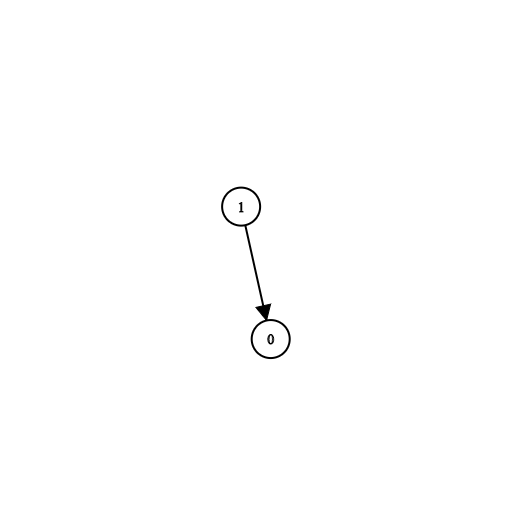
输入：n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

样例2

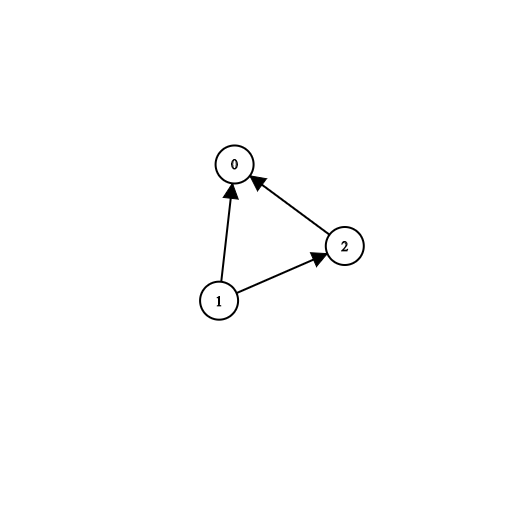
输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

题目限制

2 <= n <= 100
0 <= prerequisite.length <= (n * (n - 1) / 2)
0 <= prerequisite[i][0], prerequisite[i][1] < n
prerequisite[i][0] != prerequisite[i][1]
先修课程图中没有环。
先修课程图中没有重复的边。
1 <= queries.length <= 10^4
queries[i][0] != queries[i][1]

算法

思路

floyd骚操作——传递闭包

floyd的应用

• 最短路
• 单源多短路 ： Dijkstra | spfa
• 多源多短路 ： floyd
• 传递闭包
• 是什么 ：传递闭包的含义指通过传递性推导出尽量多的元素之间的关系
• 为什么 ：Floyd算法不仅可以实值求最短路，也可以维护关系,比如当前值能不能通过已经更新出来了的东西更新出来。具有传递性。
• 核心思想: i --> k且k --> j，那么 i -- > j
• 用邻接矩阵存，传递闭包一般都是无权图

复杂度

时间 ： $o(n ^ 3 + n)$

空间 ：$0(n ^ 2)$ 邻接矩阵

c++代码

class Solution {
public:
    vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
        vector<vector<bool>> d(n, vector<bool>(n));
        // 存下所有的边
        for(auto p: prerequisites)
            d[p[0]][p[1]] = true;
        // floyd模板 三重循环
        for(int k = 0; k < n; k++)
            for(int i = 0 ; i < n; i++)
                for(int j = 0; j < n; j++)
                    if(d[i][k] && d[k][j])
                        d[i][j] = true;

        vector<bool> res;
        for(auto q : queries)
            res.push_back(d[q[0]][q[1]]);

        return res;    
    }
};

相似题目

考察点: 有向无环图的拓扑排序

207. 课程表

// 有向无环图
// 拓扑排序 -> BFS模板 
// 入队规则 ： 入度为0即可入

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> in_dregee(numCourses, 0);
        // 计算顶点的入度 + 邻接矩阵建立图  
        for(auto p : prerequisites)
        {
            in_dregee[p[0]] ++;
            graph[p[1]].push_back(p[0]);
        }
        // BFS模板  更新每个顶点能否变为入度为0的顶点
        queue<int> q;
        vector<bool> st(numCourses, false);
        // 入度为0的顶点入队
        for(int i = 0; i < numCourses; i ++)
            if(in_dregee[i] == 0) 
                q.push(i);
        // 取队首 -> 枚举其所有出边对应的顶点 并更新该顶点的入度 若为0 则入队
        while(!q.empty())
        {
            int u = q.front();
            q.pop();
            st[u] = true;

            for(int i = 0 ; i < graph[u].size(); i ++)
            {
                in_dregee[graph[u][i]] --;
                if(in_dregee[graph[u][i]] == 0)
                    q.push(graph[u][i]);
            }
        }        
        // 判断是否都为0
        for(int i = 0; i < numCourses; i ++)
            if(st[i] == false)
                return false;

        return true;
    }
};

210. 课程表 II

// 有向无环图
// 拓扑排序 -> BFS模板 
// 入队规则 ： 入度为0即可入
// BFS的时候更新答案
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> in_degree(numCourses, 0);
        // 数对的第二个指向第一个建图
        for(auto p : prerequisites)
        {
            in_degree[p[0]] ++;
            graph[p[1]].push_back(p[0]);
        }
        // BFS 模板 维护某些值
        queue<int> q;
        vector<bool> st(numCourses,false);
        vector<int> res;

        for(int i = 0; i < numCourses; i++)    
            if(in_degree[i] == 0)
                q.push(i);

       while(!q.empty())
       {
           auto u = q.front();
           q.pop();
           st[u] = true;
           res.push_back(u); //更新答案哦

           for(int i = 0; i < graph[u].size(); i++)
           {
               in_degree[graph[u][i]] --;
               if(in_degree[graph[u][i]] == 0)  
                    q.push(graph[u][i]);
           }
       }

        // 判断每个顶点的状态
        for(auto s : st)   
               if(s == false)  return vector<int> ();

        return res; 

    }
};