题目描述

给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子(0,0)出发，机器人 2 从右上角格子 (0, cols-1)出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

从格子 (i,j) 出发，机器人可以移动到格子(i+1, j-1)，(i+1, j)或者(i+1, j+1) 。
当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到grid外面。
两个机器人最后都要到达 grid 最底下一行。

样例

样例1

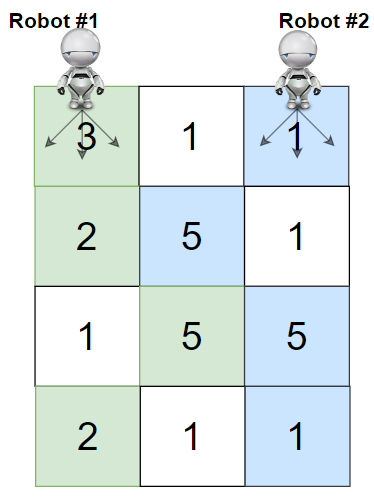
输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

样例2

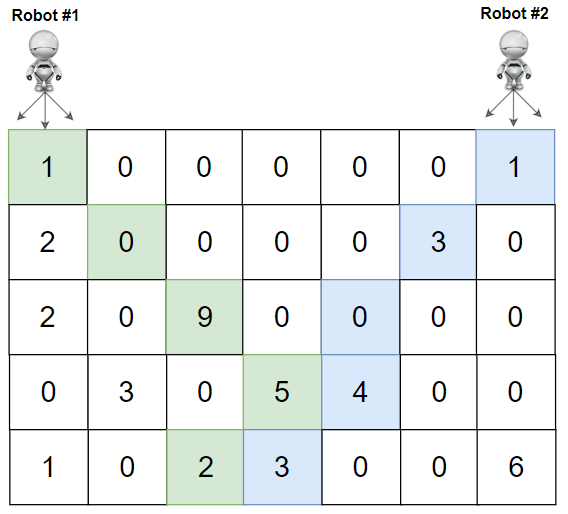
输入：grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 

限制条件

rows == grid.length
cols == grid[i].length

2 <= rows, cols <= 70
0 <= grid[i][j] <= 100

算法

思路

动态规划

状态表示：

• f(k,i,j) 表示两个机器人的位置分别位于grid(k,i) 和grid(k,j) 时的最大收益

状态计算

• 每个机器人都有三种走法，所以共有9中转移状态
• 两层for循环枚举这9中状态即可，状态合法时更新最大值
• 注意进入同一个格子只能取其一

复杂度

时间 ： $o(n^3 * 9)$

空间 ：$o(n ^ 3)$

c++代码

class Solution {
  public:
      int cherryPickup(vector<vector<int>>& grid) {
          int n = grid.size(), m = grid[0].size();
          vector<vector<vector<int>>> f(n, vector<vector<int>>(m, vector<int>(m, -1)));
          // f(k,i,j) 位置分别再grid(k,i) 和grid(k,j) 时的最大收益
          f[0][0][m - 1] = grid[0][0] + grid[0][m - 1]; 

          int res = 0;
          for (int k = 1; k < n; k ++ )
              for (int i = 0; i < m; i ++ )
                  for (int j = 0; j < m; j ++ )
                      // 9钟状态转移
                      for (int a = i - 1; a <= i + 1; a ++ )
                          for (int b = j - 1; b <= j + 1; b ++ )
                          {   // 出界
                              if (a < 0 || a >= m || b < 0 || b >= m) continue;
                              // 无收益直接跳过
                              int t = f[k - 1][a][b];
                              if (t == -1) continue;
                              // 进入同一个格子 只能选一次
                              if (i == j)  // 进入同一个格子只能选一次
                                  t += grid[k][i];
                              else 
                                  t += grid[k][i] + grid[k][j];
                              //更新状态
                              f[k][i][j] = max(f[k][i][j], t);
                              // 更新答案
                              res = max(res, f[k][i][j]);
                          }
          return res;

      }
  };

相似题目

741. 摘樱桃

• 状态表示 ：f(s,x1,x2)走了s步，第一条路线和第二条路线当前点的横坐标分别为x1, x2时取得的最大樱桃数
  • 从起点到终点一共走 2*n - 1步（因为只能向下、向右两种走法）
  • 相对应的纵坐标为 s - x1, s - x2
• 状态计算 ： 怎么抵达当前位置的
  • 两个路线同时右 f(s,x1,x2) = f(s-1,x1, x2) + grid(x1,y1) + grid(x2,y2)
  • 两个路线同时下 f(s,x1,x2) = f(s-1,x1-1, x2-1) + grid(x1,y1) + grid(x2,y2)
  • 一个右，一个下 f(s,x1,x2) = f(s-1,x1, x2 - 1) + grid(x1,y1) + grid(x2,y2)
  • 一个下，一个右 f(s,x1,x2) = f(s-1,x1-1, x2) + grid(x1,y1) + grid(x2,y2)
• 注意
  • 进入相同的格子，结果数要减一
  • 三维向量的声明

class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<vector<int>>> f(2*n - 1, vector<vector<int>> (n, vector<int>(n, INT_MIN)));
        f[0][0][0] = grid[0][0];

        for(int s = 1; s < 2 * n - 1; s ++)
            for(int x1 = 0; x1 < n; x1 ++)
                for(int x2 = 0; x2 < n; x2 ++)
                {
                    int y1 = s - x1;
                    int y2 = s - x2;
                    // 位置出界
                    if(y1 < 0 || y1 >= n || y2 < 0 || y2 >= n)
                        continue;
                    // 特殊格子进不去
                    if(grid[x1][y1] == -1 || grid[x2][y2] == -1)
                        continue;
                    // 如果走到同一个格子 只能取一个
                    int t = grid[x1][y1] + grid[x2][y2];
                    if(x1 == x2 && t > 0)
                        t--;

                    f[s][x1][x2] = f[s - 1][x1][x2] + t;

                    if(x1 > 0)
                        f[s][x1][x2] = max(f[s][x1][x2], f[s - 1][x1 - 1][x2] + t);

                    if(x2 > 0)  
                        f[s][x1][x2] = max(f[s][x1][x2], f[s - 1][x1][x2 - 1] + t);

                    if(x1 > 0 && x2 > 0)
                        f[s][x1][x2] = max(f[s][x1][x2], f[s - 1][x1 - 1][x2 - 1] + t);
                }

        return max(0, f[2*n - 2][n - 1][n - 1]);

    }
};