算法：单调栈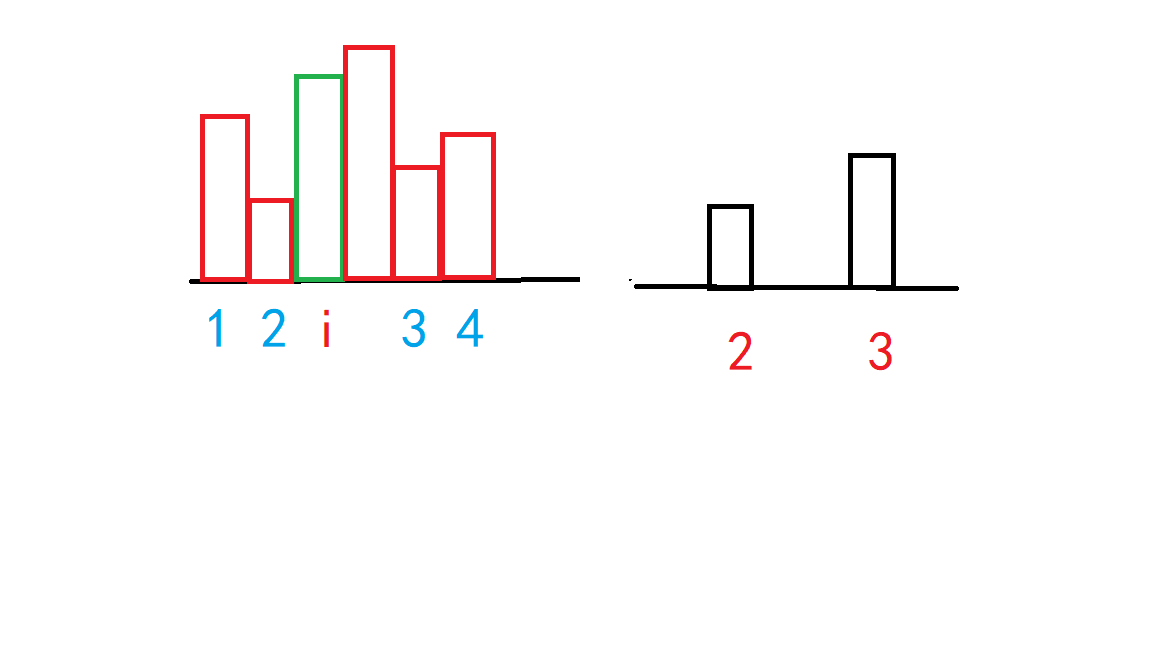

1.思路：

1.1 依次枚举1-n号矩形的高作为最大矩形的高，对于每个i确定左边最远的边界l[i]和右边最远的边界r[i],宽为r[i]-l[i]+1;
      l[i]:=(j<=i&&h[j-1]<h[i])的最大的j；
      r[i]:=(j>=i&&h[r+1]<h[i])的最小的j;

1.2 如何利用单调栈的性质快速求出对于每个i的l[i],r[i]
    在确定l[i]时，2的高小于1，1的存在没有意义，删掉1；
    在确定r[i]时，3的高小于4，4的存在没有意义，删掉4；
    总结：在查询l[i],r[i]的栈中，栈里面存的是各点的编号（不一定是连续的），但编号代表的矩形的高是单调递增的
          即单调栈；

2.边界

2.1: 每个矩形的高度都是>=0的，为了使得每个矩形的两侧都有矮于它的矩形，

     所以往两侧放了两个-1的矩形h[0] = h[n + 1] = -1;

2.2  由于有-1矩形的存在，对于左右边界的矩形，l[1]=0+1,r[n]=n+1-1,在求l数组时，stk[0]=0,h[0]==-1最小，栈非空

     在求r数组中，stk[0]=n+1,h[n+1]==-1,栈同样非空，因此可以省略栈中是否有元素的判断条件tt >= 0

3.代码1

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 100010;

//l[i], r[i]表示第i个矩形的高度可向两侧扩展的左右边界
int h[N], q[N], l[N], r[N];

typedef long long LL;

int main()
{
    int n;
    while(scanf("%d", &n), n)
    {
        for(int i = 1; i <= n; i ++)  scanf("%d", &h[i]);
        h[0] = h[n + 1] = -1;

        int tt = -1;
        q[++ tt] = 0;
        for(int i = 1; i <= n; i ++)
        {
            while(h[q[tt]] >= h[i])  tt --;
            l[i] = q[tt]+1;
            q[++ tt] = i;
        }

        tt = -1;
        q[++ tt] = n + 1;
        for(int i = n; i; i --)
        {
            while(h[q[tt]] >= h[i])  tt --;
            r[i] = q[tt]-1;
            q[++ tt] = i;
        }

        LL res = 0;
        for(int i = 1; i <= n; i ++)  res = max(res,(LL)h[i]*(r[i]-l[i]+1));
        printf("%lld\n", res);
    }
    return 0;
}